题目内容
在△ABC中,设a,b,c是角A,B,C所对的边,S是该三角形的面积,且 .
.
(I)求角B的度数;
(II)若 ,求b的值.
,求b的值.
解:(I)由
得
所以 ,
,
∵0<B<π,∴ ;
;
(II)由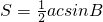 ,得
,得 ,
,
则b2=a2+c2-2accosB= ,
,
∵b>0,∴ .
.
分析:(I)利用二倍角的余弦函数公式化简已知的等式,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出B的度数;
(II)由a,cosB及三角形的面积S,利用面积公式求出c的值,然后由a,c及cosB的值,利用余弦定理即可求出b的值.
点评:此题考查了二倍角的余弦函数公式,三角形的面积公式及余弦定理,熟练掌握公式及定理是解本题的关键.

得

所以
 ,
,∵0<B<π,∴
 ;
;(II)由
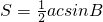 ,得
,得 ,
,则b2=a2+c2-2accosB=
 ,
,∵b>0,∴
 .
.分析:(I)利用二倍角的余弦函数公式化简已知的等式,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出B的度数;
(II)由a,cosB及三角形的面积S,利用面积公式求出c的值,然后由a,c及cosB的值,利用余弦定理即可求出b的值.
点评:此题考查了二倍角的余弦函数公式,三角形的面积公式及余弦定理,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目