题目内容
(2010•成都一模)曲线y=
在点P(1,0)处的切线方程为
| 2x-2 |
| x+2 |
y=
(x-1)
| 2 |
| 3 |
y=
(x-1)
.| 2 |
| 3 |
分析:根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,即可.
解答:解:y′=(
)′=
=
,
∴k=y′|x=1=
.
曲线y=
在点P(1,0)处的切线方程为:y=
(x-1).
故答案为:y=
(x-1).
| 2x-2 |
| x+2 |
| 2(x+2)-2x+2 |
| (x+2)2 |
| 6 |
| (x+2)2 |
∴k=y′|x=1=
| 2 |
| 3 |
曲线y=
| 2x-2 |
| x+2 |
| 2 |
| 3 |
故答案为:y=
| 2 |
| 3 |
点评:本题考查了导数的几何意义,以及导数的运算法则,本题属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目

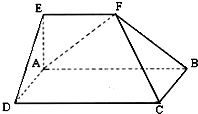 (2010•成都一模)如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
(2010•成都一模)如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.