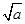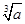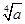题目内容
已知正数a,b,c成等差数列,且公差d≠0,求证:
,
,
不可能是等差数列.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
证明(反证法):假设
,
,
成等差数列,
则
-
=
-
,即
=
两边乘以b,得
=
又∵a,b,c成等差数列,且公差不为零,
∴a-b=b-c≠0.由以上两式,可知
=
..
两边都乘以ac,得a=c.
这与已知数列a,b,c的公差不为零,a≠c相矛盾,
所以数列
,
,
不可能成等差数列
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
则
| 1 |
| b |
| 1 |
| a |
| 1 |
| c |
| 1 |
| b |
| a-b |
| ab |
| b-c |
| cb |
| a-b |
| a |
| b-c |
| c |
又∵a,b,c成等差数列,且公差不为零,
∴a-b=b-c≠0.由以上两式,可知
| 1 |
| a |
| 1 |
| c |
两边都乘以ac,得a=c.
这与已知数列a,b,c的公差不为零,a≠c相矛盾,
所以数列
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |

练习册系列答案
相关题目
已知正数a、b、c成等比数列,则下列三数也成等比数列的是( )
| A、lga lgb lgc | ||||||||
| B、10a10b10c | ||||||||
| C、5lga5lgb5lgc | ||||||||
D、
|
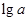
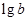
 B.
B.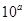

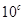 C.
C.
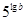
 D.
D.