题目内容
如图,在平面直角坐标系 中,
中, 为椭圆
为椭圆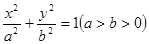 的四个顶点,F为其右焦点,直线
的四个顶点,F为其右焦点,直线 与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为
与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为
A. | B. | C. | D.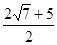 |
A
解析试题分析:直线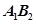 方程为
方程为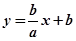 ,直线
,直线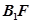 方程为
方程为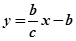 ,联立方程得
,联立方程得
 代入椭圆整理的
代入椭圆整理的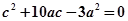 即
即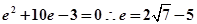
考点:椭圆离心率
点评:求离心率的值需找到关于 的齐次方程,本题思路简单,计算量较大
的齐次方程,本题思路简单,计算量较大

练习册系列答案
相关题目
抛物线 的焦点为F,倾斜角为
的焦点为F,倾斜角为 的直线
的直线 过点F且与抛物线的一个交点为A,
过点F且与抛物线的一个交点为A, ,则抛物线的方程为
,则抛物线的方程为
A. | B. |
C. 或 或 | D. 或 或 |
已知椭圆 的上、下顶点分别为
的上、下顶点分别为 、
、 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,若四边形
,若四边形 是正方形,则此椭圆的离心率
是正方形,则此椭圆的离心率 等于
等于
A. | B. | C. | D. |
抛物线y2=2Px,过点A(2,4),F为焦点,定点B的坐标为(8,-8),则|AF|∶|BF|值为
| A.1∶4 | B.1∶2 | C.2∶5 | D.3∶8 |
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
中心在坐标原点的椭圆,焦点在x轴上,焦距为4,离心率为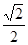 ,则该椭圆的方程为
,则该椭圆的方程为
A. | B.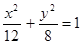 | C. | D. |
已知抛物线 的焦点为
的焦点为 ,准线与
,准线与 轴的交点为
轴的交点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
 的左、右焦点,P是双曲线左支的一点,
的左、右焦点,P是双曲线左支的一点,  ,
, ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )


