题目内容
设 ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
【答案】分析:根据题意,分析f(x)可得其是奇函数,且是增函数,进而将不等式f(m)+f(m2-2)≥0转化为f(m)≥f(2-m2),由单调性,可得其等价于m≥2-m2,解可得答案.
解答:解:根据题意,f(x)=x3+log2(x+ ),
),
f(-x)=-x3+log2(-x+ )=-x3-log2(x+
)=-x3-log2(x+ ),
),
即f(x)是奇函数,
分析单调性容易得到f(x)是增函数,
则不等式f(m)+f(m2-2)≥0?f(m)≥-f(m2-2)=f(2-m2),
由单调性又可得,该不等式等价于m≥2-m2,即m2+m-2≥0,
解可得,m≤-2或m≥1,
即(-∞,-2]∪[1,+∞)
故答案为(-∞,-2]∪[1,+∞).
点评:本题考查函数的单调性与奇偶性的综合运用,其中将不等式的恒成立与奇偶性、单调性结合,解题时,注意先分析函数的奇偶性与单调性,再转化不等式,进而求解.
解答:解:根据题意,f(x)=x3+log2(x+
 ),
),f(-x)=-x3+log2(-x+
 )=-x3-log2(x+
)=-x3-log2(x+ ),
),即f(x)是奇函数,
分析单调性容易得到f(x)是增函数,
则不等式f(m)+f(m2-2)≥0?f(m)≥-f(m2-2)=f(2-m2),
由单调性又可得,该不等式等价于m≥2-m2,即m2+m-2≥0,
解可得,m≤-2或m≥1,
即(-∞,-2]∪[1,+∞)
故答案为(-∞,-2]∪[1,+∞).
点评:本题考查函数的单调性与奇偶性的综合运用,其中将不等式的恒成立与奇偶性、单调性结合,解题时,注意先分析函数的奇偶性与单调性,再转化不等式,进而求解.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围) ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)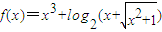 ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围) ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是 .(注:填写m的取值范围)