题目内容
已知函数f(x)=-x3-2mx2-m2x+1-m(其中m>-2)在点x=1处取得极值,
(1)求实数m的值;
(2)求函数f(x)在区间[0,1]上的最小值;
(3)若a≥0,b≥0,c≥0,且a+b+c=1,证明不等式 。
。
(1)求实数m的值;
(2)求函数f(x)在区间[0,1]上的最小值;
(3)若a≥0,b≥0,c≥0,且a+b+c=1,证明不等式
 。
。 解:(1)f′(x)=-3x2-4mx-m2,
由f′(1)=0得m2+4m+3=0,∴m=-3或m=-1,
又m>-2,
∴m=-1;
(2)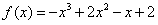 ,
,
则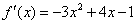 ,
,
令f′(x)=0,得f(x)在[0,1]上的增区间为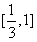 ,减区间为
,减区间为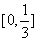 ,
,
∴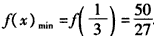 ;
;
(3)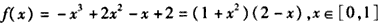 ,
,
∴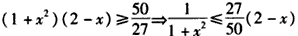 ,
,
即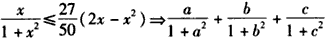
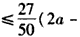
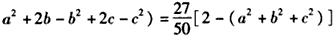 ,
,
又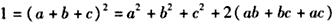
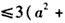
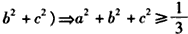 ,
,
∴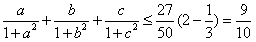 (当且仅当
(当且仅当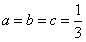 时取等号)。
时取等号)。
由f′(1)=0得m2+4m+3=0,∴m=-3或m=-1,
又m>-2,
∴m=-1;
(2)
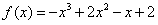 ,
,则
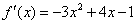 ,
,令f′(x)=0,得f(x)在[0,1]上的增区间为
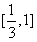 ,减区间为
,减区间为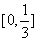 ,
,∴
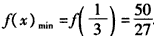 ;
;(3)
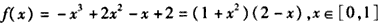 ,
,∴
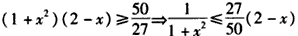 ,
,即
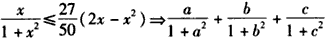
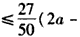
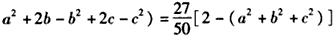 ,
,又
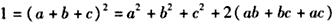
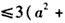
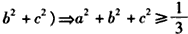 ,
,∴
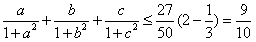 (当且仅当
(当且仅当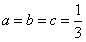 时取等号)。
时取等号)。 
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|