题目内容
例3:已知数列{an}的前n项和为Sn,对于任意的自然数n,均有| Sn |
| n |
| 1 |
| 2 |
分析:通过
=
an分别求出an+1和an的值,二者相减进而求出2an=an+1+an-1根据等差数列的等差性质证明出{an}为等差数列.
| Sn |
| n |
| 1 |
| 2 |
解答:证明:∵
=
an
∴an+1=Sn+1-Sn=
•an-
•an①
∴an=Sn-Sn-1=
•an-
•an-1②
①-②得
an+1-an=
•an+1-
•an-1-nan
即2an=an+1+an-1
∴数列{an}为等差数列
| Sn |
| n |
| 1 |
| 2 |
∴an+1=Sn+1-Sn=
| n+1 |
| 2 |
| n |
| 2 |
∴an=Sn-Sn-1=
| n |
| 2 |
| n-1 |
| 2 |
①-②得
an+1-an=
| n+1 |
| 2 |
| n-1 |
| 2 |
即2an=an+1+an-1
∴数列{an}为等差数列
点评:本题主要考查了数列求和和等差数列的等差性质.属基础题.

练习册系列答案
相关题目
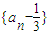 是等比数列.
是等比数列. an成立,试证明数列{an}为等差数列.
an成立,试证明数列{an}为等差数列.