题目内容
已知函数f(x)的定义域为R,对任意实数m,n都有 ,且
,且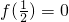 ,当
,当 时,f(x)>0.
时,f(x)>0.
(1)求f(1);
(2)求和f(1)+f(2)+…+f(n)(n∈N*);
(3)判断函数f(x)的单调性并证明.
解:(1)f(1)=f( )+f(
)+f( )+
)+ =0+0+
=0+0+ =
= ,
,
(2)∵f(2)=f(1)+f(1)+ =3×
=3× ,
,
f(3)=f(2)+f(1)=5× ,
,
f(n)=(2n-1)× ,
,
∴f(1)+f(2)+…+f(n)= (1+3+5+…(2n-1))=
(1+3+5+…(2n-1))= n2
n2
(3)f(x)=( 2x-1)× =x-
=x- ,在其定义域内是增函数,
,在其定义域内是增函数,
证明:设 a<b,f(b)-f(a)=(b- )-(a-
)-(a- )=b-a,由题设知,b-a>0,
)=b-a,由题设知,b-a>0,
∴f(b)-f(a)>0,f(b),>f(a),∴f(x)在其定义域内是增函数.
分析:(1)在已知等式中,令m=n= ,可以求出f(1)的值.
,可以求出f(1)的值.
(2)由f(1)的值和已知等式,依次求出f(2)、f(3)、…f(n),利用等差数列的求和公式计算出所求式子的值.
(3)写出f(x)的解析式,依据单调性的定义证明在其定义域内单调递增.
点评:本题考查抽象函数的应用、数列求和、函数的单调性的证明.
 )+f(
)+f( )+
)+ =0+0+
=0+0+ =
= ,
,(2)∵f(2)=f(1)+f(1)+
 =3×
=3× ,
,f(3)=f(2)+f(1)=5×
 ,
,f(n)=(2n-1)×
 ,
,∴f(1)+f(2)+…+f(n)=
 (1+3+5+…(2n-1))=
(1+3+5+…(2n-1))= n2
n2(3)f(x)=( 2x-1)×
 =x-
=x- ,在其定义域内是增函数,
,在其定义域内是增函数,证明:设 a<b,f(b)-f(a)=(b-
 )-(a-
)-(a- )=b-a,由题设知,b-a>0,
)=b-a,由题设知,b-a>0,∴f(b)-f(a)>0,f(b),>f(a),∴f(x)在其定义域内是增函数.
分析:(1)在已知等式中,令m=n=
 ,可以求出f(1)的值.
,可以求出f(1)的值.(2)由f(1)的值和已知等式,依次求出f(2)、f(3)、…f(n),利用等差数列的求和公式计算出所求式子的值.
(3)写出f(x)的解析式,依据单调性的定义证明在其定义域内单调递增.
点评:本题考查抽象函数的应用、数列求和、函数的单调性的证明.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
