Question

设函数f(x)=2sinxcosx-cos(2x-

π

6

)．
（Ⅰ）求函数f（x）的最小正周期；
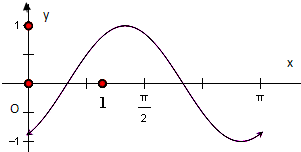
（Ⅱ）画出函数f（x）在区间[0，π]上的图象；
（Ⅲ）当x∈[0，

2π

3

]时，求函数f（x）的最大值及取得最大值时的x的值．

Answer 1

分析：（I）先利用两角差的余弦公式及二倍角公式对已知函数进行化简，然后结合周期公式即可求解
（II）结合正弦函数的性质即可求解
（III）由已知x的范围求出2x-

1

3

π的范围，然后结合正弦函数的性质可求函数的最值

解答：解：（Ⅰ）因为f(x)=2sinxcosx-cos(2x-

π

6

)
=sin2x-(cos2xcos

π

6

+sin2xsin

π

6

)
=

1

2

sin2x-

3

2

cos2x=sin(2x-

π

3

)，…（3分）
所以f(x)=sin(2x-

π

3

)．
函数f（x）的最小正周期为π…（4分）
（Ⅱ）图象如图所示（8分）
（Ⅲ）因为x∈[0，

2π

3

]，所以2x-

π

3

∈[-

π

3

，π]．
所以，当2x-

π

3

=

π

2

，即x=

5π

12

时 …10函数f（x）的最大值为1  …（12分）

点评：本题主要考查了两角和的三角公式及正弦函数的性质的简单应用，属于基础试题