题目内容
设曲线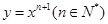 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为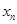 ,则
,则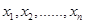 的乘积的值为( )
的乘积的值为( )
A.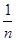 | B.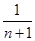 | C.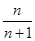 | D.1 |
B
解析试题分析:对y=xn+1(n∈N*)求导得y′=(n+1)xn,
令x=1得在点(1,1)处的切线的斜率k=n+1,在点
(1,1)处的切线方程为y-1=k(xn-1)=(n+1)(xn-1),
不妨设y=0,xn= 则x1•x2•x3…•xn=
则x1•x2•x3…•xn= ,
,
故选B..
考点:利用导数研究曲线上某点切线方程;直线的斜率..

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知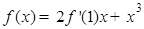 ,则
,则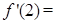 ( )
( )
A. | B.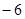 | C.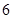 | D.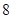 |
设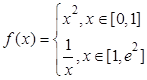 (其中e为自然对数的底数),则
(其中e为自然对数的底数),则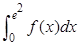 的值为( )
的值为( )
A.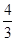 | B.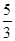 | C.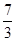 | D.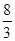 |
已知函数 ,
, 是函数
是函数 的导函数,且
的导函数,且 有两个零点
有两个零点 和
和 (
( ),则
),则 的最小值为()
的最小值为()
A. | B. | C. | D.以上都不对 |
函数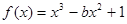 有且仅有两个不同的零点,则
有且仅有两个不同的零点,则 的值为( )
的值为( )
A.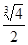 | B.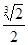 | C.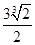 | D.不确定 |
若S1=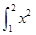 dx,S2=
dx,S2=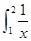 dx,S3=
dx,S3=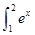 dx,则S1,S2,S3的大小关系为( )
dx,则S1,S2,S3的大小关系为( )
| A.S1<S2<S3 | B.S2<S1<S3 |
| C.S2<S3<S1 | D.S3<S2<S1 |
设f(x)=(ax+b)sinx+(cx+d)cosx,若已知f′(x)=xcosx,则f(x)=( )
| A.xsinx |
| B.xsinx-xcosx |
| C.xsinx+cosx |
| D.xcosx |
某公司生产一种产品,固定成本为20000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )
| A.150 |
| B.200 |
| C.250 |
| D.300 |
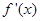 是f(x)的导函数,
是f(x)的导函数,