题目内容
已知数列{an} 为等比数列,且 则
则 的值为
的值为
- A.

- B.

- C.
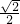
- D.

B
分析:根据等比数列的性质化简已知的等式,开立方即可得到a7的值,然后再根据等比数列的性质化简所求的式子,得到关于a7的关系式,把a7的值代入,利用诱导公式及特殊角的三角函数值即可求出值.
解答:根据等比数列的性质得:a1•a13=a72,
所以a1•a7•a13=a73= ,得到a7=
,得到a7= ,
,
则 =cos|a7|=cos
=cos|a7|=cos =cos(
=cos( )=-cos
)=-cos =-
=- .
.
故选B
点评:此题考查学生掌握等比数列的性质,灵活运用诱导公式及特殊角的三角函数值化简求值,是一道基础题.
分析:根据等比数列的性质化简已知的等式,开立方即可得到a7的值,然后再根据等比数列的性质化简所求的式子,得到关于a7的关系式,把a7的值代入,利用诱导公式及特殊角的三角函数值即可求出值.
解答:根据等比数列的性质得:a1•a13=a72,
所以a1•a7•a13=a73=
 ,得到a7=
,得到a7= ,
,则
 =cos|a7|=cos
=cos|a7|=cos =cos(
=cos( )=-cos
)=-cos =-
=- .
.故选B
点评:此题考查学生掌握等比数列的性质,灵活运用诱导公式及特殊角的三角函数值化简求值,是一道基础题.

练习册系列答案
相关题目
已知数列{an}为等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为
,则S5=( )
| 5 |
| 4 |
| A、35 | B、33 | C、31 | D、29 |
已知数列{an}为等差数列,a1+a3+a5=15,a4=7,则s6的值为( )
| A、30 | B、35 | C、36 | D、24 |