题目内容
如图，直线l1、l2、l3的斜率分别为k1、k2、k3，则必有
- A.k1＜k3＜k2
- B.k3＜k1＜k2
- C.k1＜k2＜k3
- D.k3＜k2＜k1
A
分析：先由图得出三直线倾斜角的关系，再根据正切函数的性质，判断斜率的大小关系．
解答：设直线l1、l2、l3的倾斜角分别为α1，α2，α3．由已知为α1为钝角，α2＞α3，且均为锐角．
由于正切函数y=tanx在（0，
）上单调递增，且函数值为正，所以tanα2＞tanα3＞0，即k2＞k3＞0．
当α为钝角时，tanα为负，所以k1=tanα1＜0．
综上k1＜k3＜k2，
故选A．
点评：本题考查直线倾斜角和斜率的关系：k=tanα，研究的方法就是利用正切函数的性质．
分析：先由图得出三直线倾斜角的关系，再根据正切函数的性质，判断斜率的大小关系．
解答：设直线l1、l2、l3的倾斜角分别为α1，α2，α3．由已知为α1为钝角，α2＞α3，且均为锐角．
由于正切函数y=tanx在（0，
）上单调递增，且函数值为正，所以tanα2＞tanα3＞0，即k2＞k3＞0．当α为钝角时，tanα为负，所以k1=tanα1＜0．
综上k1＜k3＜k2，
故选A．
点评：本题考查直线倾斜角和斜率的关系：k=tanα，研究的方法就是利用正切函数的性质．
练习册系列答案
相关题目
如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1．以A，B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=
如图，直线l1、l2、l3的斜率分别为k1、k2、k3，则必有（ ）
如图，直线l1和l2相交于点M且l1⊥l2，点N∈l1．以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，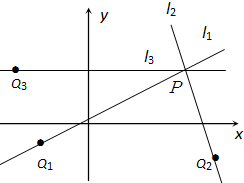
如图，直线l1，l2，l3，都经过点P（3，2），又l1，l2，l3分别经过点Q1（-2，-1），Q2（4，-2），Q3（-3，2），试计算直线l1，l2，l3的斜率．
如图，直线l1，l2，l3的斜率分别为k1，k2，k3，则（ ）