题目内容
下列命题:
①若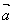 与
与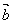 共线,
共线, 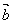 与
与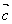 共线,则
共线,则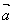 与
与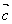 共线;
共线;
②向量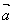 、
、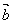 、
、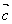 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③若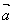 与
与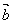 共线,则存在唯一的实数
共线,则存在唯一的实数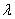 ,使
,使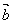 =
=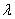
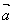 ;
;
④若A、B、C三点不共线,0是平面ABC外一点.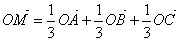 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,
上述命题中的真命题是 .
【答案】
④ 解析:如果 =
= ,则
,则 与
与 不一定共线,
不一定共线,
所以①错误;因为向量可以任意平移,可知②错;
③中的 ≠
≠ 这一条件缺少,于是③错.
这一条件缺少,于是③错.
可以证明④中A、B、C、M四点共面.等式两边同加 ,
,
则 =0,即
=0,即
 ,则
,则 与
与 、
、 共面,又M是三个有向线段的公共点,故A、B、C、M四点共面.故④是真命题.
共面,又M是三个有向线段的公共点,故A、B、C、M四点共面.故④是真命题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
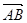 与
与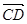 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;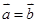 ,
, 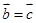 ,则
,则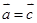 ;
;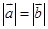 ,则
,则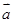 与
与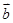 共线,
共线, 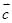 共线,则
共线,则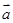 与
与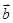 为非零向量,下列命题:
为非零向量,下列命题: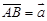 ,
,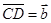 ,
,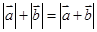 ;
;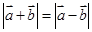 ,则
,则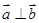 ;
;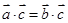 ,
,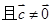 ,则
,则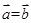
 、
、 、
、 、
、 是空间四个不同的点,在下列命题中,不正确的是(
)
是空间四个不同的点,在下列命题中,不正确的是(
) 与
与 共面,则
共面,则 与
与 共面
共面 ,
, ,则
,则

 、
、 、
、 、
、 是空间四个不同的点,在下列命题中,不正确的是( )
是空间四个不同的点,在下列命题中,不正确的是( ) 与
与 共面,则
共面,则 与
与 共面
共面 ,
, ,则
,则

 =0,则
=0,则 =0;
=0; ;
; 是三个非零向量,若
是三个非零向量,若 ,则|
,则| |=|
|=| |;
|; =λ1
=λ1 +λ2
+λ2 ,则
,则 共线
共线
 .
.