Question

在正方体ABCD-A₁B₁C₁D₁中，过对角线BD₁的一个平面交AA₁于E，交CC₁于F，则面BFD₁E与底面A₁B₁C₁D₁所成的二面角的最小值为

π

4

．

Answer 1

分析：在平面AA₁D₁D中，过E作EH⊥D₁D于H，过H作HG⊥D₁F于G，连接EG．根据线面垂直的判定与性质，可证出∠EGH就是面BFD₁E与底面A₁B₁C₁D₁所成的二面角的平面角．设正方体棱长为1，C₁F=x，利用三角形相似算出HG=

1-x

1+x2

，再结合Rt△EGH中正切的定义，可得当HG取最大值1时，面BFD₁E与底面A₁B₁C₁D₁所成的二面角取到最小值

π

4

．

解答：解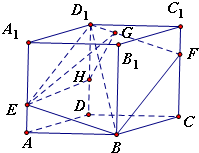：在平面AA₁D₁D中，过E作EH⊥D₁D于H，过H作HG⊥D₁F于G，连接EG
∵平面AA₁D₁D⊥平面CC₁D₁D，平面AA₁D₁D∩平面CC₁D₁D=EH，EH⊥D₁D
∴EH⊥平面CC₁D₁D，
∵D₁F⊆平面CC₁D₁D，∴D₁F⊥EH
∵HG⊥D₁F，EH、HG是平面EHG内的相交直线
∴D₁F⊥平面EHG
∵GE⊆平面EHG，
∴EG⊥D₁F，可得∠EGH就是面BFD₁E与底面A₁B₁C₁D₁所成的二面角的平面角
设正方体棱长为1，C₁F=x，得AE=DH=x，D₁H=1-x，（0≤x≤1）
∵Rt△D₁GH∽Rt△FC₁D₁，
∴

HG

D1C1

=

D1H

D1F

，得HG=

1-x

1+x2

而函数f（x）=

1-x

1+x2

在区间（0，1）上是减函数，可得当x=0时HG有最大值1，当x=1时HG有最小值0．
∵Rt△EGH中，tan∠EGH=

EH

HG

=

1

EG

∴当HG取最大值1时，tan∠EGH有最小值1，
此时∠EGH也有最小值

π

4

，即面BFD₁E与底面A₁B₁C₁D₁所成的二面角的最小值为

π

4

故答案为：

π

4

点评：本题在正方体中给出运动的截面，求二面角的最小值，着重考查了空间线面垂直的判定与性质和二面角大小的求法等知识，属于中档题．