题目内容
已知函数f(x)=ax2-x(a∈R,a≠0),g(x)=lnx
(1)当a=1时,判断函数f(x)-g(x)在定义域上的单调性;
(2)若函数y=f(x)与y=g(x)的图象有两个不同的交点M,N,求a的取值范围.
(3)设点A(x1,y1)和B(x2,y2)(x1<x2)是函数y=g(x)图象上的两点,平行于AB的切线以P(x0,y0)为切点,求证x1<x0<x2.
解:(1)记F(x)=f(x)-g(x)=ax2-x-lnx,(x>0)
当a=1时,F'(x)=2ax-1- =
=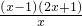 ,(x>0)
,(x>0)
∵当x∈(0,1)时F'(x)<0;当x∈(1,+∞)时F'(x)>0
∴函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);
(2)函数y=f(x)与y=g(x)的图象的交点横坐标,即为方程f(x)=g(x)的实数解
由f(x)=g(x),得ax2-x=lnx,可得a=
令r(x)= ,求导数得r'(x)=
,求导数得r'(x)= =
=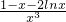
∵当x∈(0,1)时r'(x)>0;当x∈(1,+∞)时r'(x)<0
∴函数r(x)的单调增区间为(0,1),单调减区间为(1,+∞),
可得r(x)的极大值为r(1)=1>0,
又∵r( )=
)=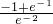 <0,当x→0时,r(x)→-∞,且当x>1时0<r(x)<1
<0,当x→0时,r(x)→-∞,且当x>1时0<r(x)<1
∴r(1)=1是函数r(x)的最大值,且函数r(x)的值域为(-∞,1]
因此,要使y=f(x)与y=g(x)图象有两个不同的交点M、N,实数a的取值范围为(0,1).
(3)由已知,得 =
= ,所以x0=
,所以x0=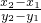 =
=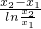 ;
;
∵函数y=ln(1+x)-x在区间(-1,0)上是减函数,在区间(0,+∞)上是增函数
∴函数y=ln(1+x)-x的最小值为0,得当x>0时,ln(1+x)-x>0,可得ln(1+x)>x
因此,由ln =ln(1+
=ln(1+ -1)<
-1)< -1,故x0=
-1,故x0=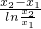 >
> =x1;
=x1;
同理可得x0=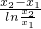 =
= =
= <
< =x2
=x2
综上所述,可得x1<x0<x2.
分析:(1)记F(x)=f(x)-g(x)=ax2-x-lnx,可得F'(x)=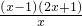 .再讨论F'(x)的正负,可得函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);
.再讨论F'(x)的正负,可得函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);
(2)由f(x)=g(x)得ax2-x=lnx,可得a= .设r(x)=
.设r(x)= ,通过研究r'(x)的正负,得到r(x)的极大值为r(1)=1>0,当x∈(0,1)时,r(x)∈(-∞,1];且当x>1时0<r(x)<1.由此可得当y=f(x)与y=g(x)图象有两个不同的交点M、N时,实数a的取值范围为(0,1);
,通过研究r'(x)的正负,得到r(x)的极大值为r(1)=1>0,当x∈(0,1)时,r(x)∈(-∞,1];且当x>1时0<r(x)<1.由此可得当y=f(x)与y=g(x)图象有两个不同的交点M、N时,实数a的取值范围为(0,1);
(3)根据导数的几何意义与两点连线的斜率公式,得 =
= ,解出x0=
,解出x0=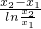 ,利用函数y=ln(1+x)-x的单调性,得出ln
,利用函数y=ln(1+x)-x的单调性,得出ln <
< -1,从而得到x0>
-1,从而得到x0> =x1;类似的方法可证出x0=
=x1;类似的方法可证出x0= <
< =x2.由此即可得到x1<x0<x2成立.
=x2.由此即可得到x1<x0<x2成立.
点评:本题给出含有字母参数的二次函数f(x)和对数函数g(x),讨论它们的差函数的单调区间,并且讨论了两个函数图象交点个数的问题.着重考查了基本初等函数的性质、利用导数研究函数的单调性、导数的几何意义与直线的斜率和不等式的证明等知识,属于中档题.
当a=1时,F'(x)=2ax-1-
 =
=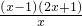 ,(x>0)
,(x>0)∵当x∈(0,1)时F'(x)<0;当x∈(1,+∞)时F'(x)>0
∴函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);
(2)函数y=f(x)与y=g(x)的图象的交点横坐标,即为方程f(x)=g(x)的实数解
由f(x)=g(x),得ax2-x=lnx,可得a=

令r(x)=
 ,求导数得r'(x)=
,求导数得r'(x)= =
=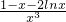
∵当x∈(0,1)时r'(x)>0;当x∈(1,+∞)时r'(x)<0
∴函数r(x)的单调增区间为(0,1),单调减区间为(1,+∞),
可得r(x)的极大值为r(1)=1>0,
又∵r(
 )=
)=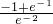 <0,当x→0时,r(x)→-∞,且当x>1时0<r(x)<1
<0,当x→0时,r(x)→-∞,且当x>1时0<r(x)<1∴r(1)=1是函数r(x)的最大值,且函数r(x)的值域为(-∞,1]
因此,要使y=f(x)与y=g(x)图象有两个不同的交点M、N,实数a的取值范围为(0,1).
(3)由已知,得
 =
= ,所以x0=
,所以x0=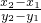 =
=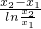 ;
;∵函数y=ln(1+x)-x在区间(-1,0)上是减函数,在区间(0,+∞)上是增函数
∴函数y=ln(1+x)-x的最小值为0,得当x>0时,ln(1+x)-x>0,可得ln(1+x)>x
因此,由ln
 =ln(1+
=ln(1+ -1)<
-1)< -1,故x0=
-1,故x0=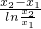 >
> =x1;
=x1;同理可得x0=
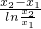 =
= =
= <
< =x2
=x2综上所述,可得x1<x0<x2.
分析:(1)记F(x)=f(x)-g(x)=ax2-x-lnx,可得F'(x)=
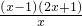 .再讨论F'(x)的正负,可得函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);
.再讨论F'(x)的正负,可得函数f(x)-g(x)的单调增区间为(1,+∞),单调减区间为(0,1);(2)由f(x)=g(x)得ax2-x=lnx,可得a=
 .设r(x)=
.设r(x)= ,通过研究r'(x)的正负,得到r(x)的极大值为r(1)=1>0,当x∈(0,1)时,r(x)∈(-∞,1];且当x>1时0<r(x)<1.由此可得当y=f(x)与y=g(x)图象有两个不同的交点M、N时,实数a的取值范围为(0,1);
,通过研究r'(x)的正负,得到r(x)的极大值为r(1)=1>0,当x∈(0,1)时,r(x)∈(-∞,1];且当x>1时0<r(x)<1.由此可得当y=f(x)与y=g(x)图象有两个不同的交点M、N时,实数a的取值范围为(0,1);(3)根据导数的几何意义与两点连线的斜率公式,得
 =
= ,解出x0=
,解出x0=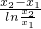 ,利用函数y=ln(1+x)-x的单调性,得出ln
,利用函数y=ln(1+x)-x的单调性,得出ln <
< -1,从而得到x0>
-1,从而得到x0> =x1;类似的方法可证出x0=
=x1;类似的方法可证出x0= <
< =x2.由此即可得到x1<x0<x2成立.
=x2.由此即可得到x1<x0<x2成立.点评:本题给出含有字母参数的二次函数f(x)和对数函数g(x),讨论它们的差函数的单调区间,并且讨论了两个函数图象交点个数的问题.着重考查了基本初等函数的性质、利用导数研究函数的单调性、导数的几何意义与直线的斜率和不等式的证明等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目