题目内容
（本小题满分12分）
已知数列{an}和{bn}满足： a1=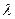
，an+1=
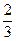an+n-4，bn=（-1）n（an-3n+21），其中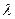为实数，n为正整数.
（Ⅰ）证明：对
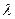任意实数，数列{an}不是等比数列；
（Ⅱ）证明：当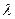≠-18时，数列{bn}是等比数列.
解
：（Ⅰ）证明 假设存在一个实数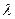，使{an}是等比数列，则有a22= a1a3，…（2分）
即
矛盾.
所以 对于任意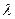，{an}不是等比数列. ……………………………（6分）
(Ⅱ)证明 因为bn+1=(-1)n+1［an+1-3（n+1）+21］="(-1)" n+1
=-
……………………………………（10分）
又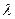≠-18，所以b1=-(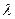+18)≠0. ……………………………………（11分）
由上式知bn≠0，所以
故当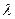≠-18时，数列{ bn}是以-(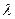+18)为首项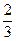，-为公比的等比数列.…（12分）
解析
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
