题目内容
(本题满分14分)集合A是由适合以下性质的函数f(x)构成的:对于定义域内任意两个不相等的实数 ,都有
,都有 .
.
(1)试判断f(x)= x2及g(x)=log2x是否在集合A中,并说明理由;
(2)设f(x)ÎA且定义域为(0,+¥),值域为(0,1), ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.
【答案】
(1) ,
, ;(2)
;(2) 。
。
【解析】
试题分析:(1) ,
, .
…………………… 2分
.
…………………… 2分
对于 的证明. 任意
的证明. 任意 且
且 ,
,

即 . ∴
. ∴ ………………… 4分
………………… 4分
对于 ,举反例:当
,举反例:当 ,
, 时,
时,
 ,
,
 ,
,
不满足 . ∴
. ∴ . ………………………6分
. ………………………6分
⑵函数 ,当
,当 时,值域为
时,值域为 且
且 .…… 8分
.…… 8分
任取 且
且 ,则
,则

即 .∴
.∴ . …………………14分
. …………………14分
考点:二次函数的性质;对数函数的性质;函数的定义域、值域;
点评:本题中 构造类型
构造类型
 或
或
 为常见,也是做此题的关键,此题难度相对较高。
为常见,也是做此题的关键,此题难度相对较高。

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 (
( 为自然对数的底数).
为自然对数的底数). 的最小值;
的最小值; 的解集为
的解集为 ,若
,若 且
且 求实数
求实数 的取值范围;
的取值范围; ,且
,且 ,是否存在等差数列
,是否存在等差数列 和首项为
和首项为 公比大于0的等比数列
公比大于0的等比数列 ,使得
,使得 ?若存在,请求出数列
?若存在,请求出数列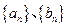 的通项公式.若不存在,请说明理由.
的通项公式.若不存在,请说明理由. ,当
,当 时,
时, ;
; 时,
时, .
. 在
在 内的值域;
内的值域; 为何值时,
为何值时, 的解集为
的解集为 .
. 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。 的解析式;
的解析式;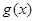 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得 的值域也是
的值域也是 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明); 时,问
时,问 的解集A;
的解集A; 的不等式
的不等式 的解集为
的解集为 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.