Question

在等差数列{a_n}中,S₁₀=100,S₁₀₀=10.求S₁₁₀.

   

Answer 1

思路分析：本题最基本的方法是设基本量,若从等差数列的不同性质出发,可以得到不同的解法.

    解法一(基本量法):设等差数列{a_n}的首项为a₁,公差为d,则

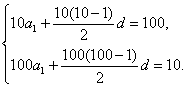
    解得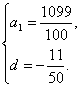

∴S₁₁₀=110a₁+d

=110×+×(-)=-110.

    解法二(设而不求整体代换法):∵S₁₀=100,S₁₀₀=10,

∴S₁₀₀-S₁₀=a₁₁+a₁₂+…+a₁₀₀=分 90(a₁₁+a₁₀₀)2式=-90.∴a₁₁+a₁₀₀=-2.

    又∵a₁+a₁₁₀=a₁₁+a₁₀₀=-2,

∴S₁₁₀==-110.

    解法三(新数列法):∵S₁₀,S₂₀-S₁₀,S₃₀-S₂₀,…,S₁₀₀-S₉₀,S₁₁₀-S₁₀₀,…成等差数列,

∴设公差为d,该数列前100项和为10×100+d=10,解得d=-22.

∴前110项和S₁₁₀=11×100+d=11×100+×(-22)=-110.

    解法四(运用函数观点解决问题):由于f(n)=是关于n的一次函数,

而点(10,),(100,),(110,)在其图象上,由斜率相等,得

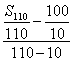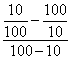
=S₁₁₀=-110.

    解法五(待定系数法):设{a_n}的前n项和S_n=An²+Bn(A、B为常数)时,

S₁₀=A×10²+B×10=100,

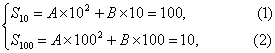
    解得A=-,B=.

∴S₁₁₀=A×110²+B×110=-×110²+×110=-110.