题目内容
(本小题满分12分)
如图5,在直三棱柱![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
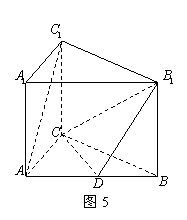 (1)求证:
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 夹角的余弦值.
夹角的余弦值.
(1)证明:设![]() 交于点O,则O为
交于点O,则O为![]() 的中点.
的中点.
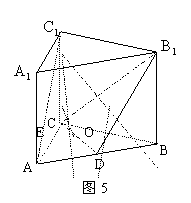 在△
在△![]() 中,连接OD,D,O分别为AB,
中,连接OD,D,O分别为AB,![]() 的中点,故OD为△
的中点,故OD为△![]() 的中位线,
的中位线,
![]() ∥
∥![]() ,又
,又![]()
![]() ,
,![]() ,
,![]() ∥平面
∥平面![]() .……6分
.……6分
(2)解法一:过![]() 作
作![]() 于
于![]() ,连接
,连接![]() .由
.由![]() 底面
底面![]() 可得
可得![]() .
.
故∠![]() 为二面角
为二面角![]() --
--![]() --
--![]() 的平面角.在△
的平面角.在△![]() 中,
中,![]() △
△![]()
 中,tan∠
中,tan∠![]() =
=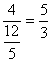 ,
,![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .………12分
.………12分
解法二:∵直三棱柱![]() 底面三边长AC=3,BC=4,AB=5,
底面三边长AC=3,BC=4,AB=5,
∴AC,BC,![]() 两两垂直.
两两垂直.
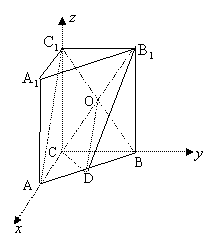
如图,以C为坐标原点,建立空间直角坐标系C-![]() ,
,
则C(0,0,0),A(3,0,0),![]() (0,0,4),B(0,4,0),
(0,0,4),B(0,4,0),
![]() (0,4,4).
(0,4,4).
平面ABC的一个法向量为![]() ,设平面
,设平面![]() AB的一个
AB的一个
法向量为![]() ,
,
![]() 由
由![]() 得
得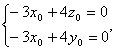 令
令![]()
则![]() .故
.故![]()
∴平面![]() 和平面
和平面![]() 夹角的余弦值为
夹角的余弦值为![]() . ……………12分
. ……………12分

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目