题目内容
已知α、β是三次函数 的两个极值点,且α∈(0,1),β∈(1,2),则
的两个极值点,且α∈(0,1),β∈(1,2),则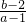 的取值范围是________.
的取值范围是________.

分析:求出导函数,据韦达定理求出α,β与a,b的关系,据α,β的范围求出a,b的范围,画出关于a,b的不等式组的可行域,由图数形结合求出
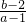 的范围.
的范围.解答:
 解:f′(x)=x2+ax+2b
解:f′(x)=x2+ax+2b∵α,β是f(x)的极值点,
所以α,β是x2+ax+2b=0的两个根
∴α+β=-a,αβ=2b
∵α∈(0,1),β∈(1,2),
∴1<α+β<3,0<αβ<2
∴1<-a<3,0<2b<2
∴

作出不等式组∴
 的可行域
的可行域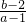 表示可行域中的点与(1,2)连线的斜率
表示可行域中的点与(1,2)连线的斜率有图知,当当点为(-3,1)和(-1,0)时分别为斜率的最小、最大值
所以此时两直线的斜率分别是

故答案为
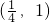
点评:本题考查函数在极值点处的值为0;利用线性规划求函数的最值,关键是给目标函数几何意义.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )