题目内容

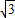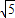空间一点P到三条两两垂直的射线OA，OB，OC的距离分别是，2，，且垂足分别是A1，B1，C1，则三棱锥P-A1B1C1的体积为（ ）
A．
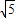
B．
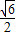
C．
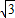
D．
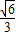
【答案】分析：由已知，P，A1，B1，C1，四点可以是一个长方体的四个顶点，利用数据求出长方体长宽高，再利用体积公式计算三棱锥P-A1B1C1的体积．
解答：解：由已知，构造出如图所示的长方体．
设长方体长宽高分别为a，b，c则
a2+b2=3，a2+c2=4，c2+a2=5
解得a=1，，c=
三棱锥P-A1B1C1的体积等于长方体体积减去以三棱锥P-A1B1C1的四个面为底面的四个小三棱锥的体积．
这四个小三棱锥的体积相等，均为

所以V=-=
故选D
点评：本题考查几何体体积的计算，本题构造出长方体是关键．并且在计算过程中采用了间接法．需具有空间想象，转化计算等能力．
练习册系列答案
相关题目
15、给出命题：
（1）在空间里，垂直于同一平面的两个平面平行；
（2）设l，m是不同的直线，α是一个平面，若l⊥α，l∥m，则m⊥α；
（3）已知α，β表示两个不同平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；
（4）若点P到三角形三个顶点的距离相等，则点P在该三角形所在平面内的射影是该三角形的外心；
（5）a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一个平行．
其中正确的命题是
（2）（4）
（只填序号）．
空间一点P到三条两两垂直的射线OA，OB，OC的距离分别是
3
，2，
5
，且垂足分别是A1，B1，C1，则三棱锥P-A1B1C1的体积为（　　）

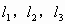是三条两两互相垂直的直线，它们相交于点O，空间一点P到的距离分别为a，b，c，则P到O的距离是________．
空间一点P到三条两两垂直的射线OA，OB，OC的距离分别是
3
，2，
5
，且垂足分别是A1，B1，C1，则三棱锥P-A1B1C1的体积为（　　）
A．
5
B．
6
2
C．
3
D．
6
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网