题目内容

已知x,y,z均为正实数,且4xy+z2+2yz+2xz=8,则x+y+z的最小值是

A.8                  B.4                   C.2                    D.2

D

解析:4xy+z2+2yz+2×z=8(2x+z)(2y+z)=82x+z=x=,

∴x+y+z=+y+=+≥2,

当且仅当(2y+z)2=8,即2y+z=2时,(x+y+z)min=22.

练习册系列答案
相关题目
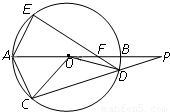
【选做题】在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．
A．选修4-1　几何证明选讲
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．选修4-2　矩阵与变换
若点A（2，2）在矩阵M=
cosα-sinα
sinαcosα
对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵．
C．选修4-4　坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，
曲线C1：ρcos(θ+
π
4
)=2
2
与曲线C2：
x=4t2
y=4t
（t∈R）交于A、B两点．求证：OA⊥OB．
D．选修4-5　不等式选讲
已知x，y，z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
A．如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．已知矩阵A=
.
1-2
3-7
.
．
（1）求逆矩阵A-1；
（2）若矩阵X满足AX=
3
1
，试求矩阵X．
C．坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C1：ρcos（θ+
π
4
）=2
2
与曲线C2：
x=4t2
y=4t
，（t∈R）交于A、B两点．求证：OA⊥OB．
D．已知x，y，z均为正数，求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．

已知x、y、z均为正实数，且3x＝4y＝6x，求证
A．如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．已知矩阵A=．
（1）求逆矩阵A-1；
（2）若矩阵X满足，试求矩阵X．
C．坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C1：ρcos（θ+）=2与曲线C2：
，（t∈R）交于A、B两点．求证：OA⊥OB．
D．已知x，y，z均为正数，求证：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网