题目内容
已知函数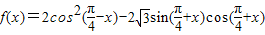 .
.(1)求
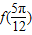 的值;
的值;(2)求f(x)的单调减区间;
(3)若
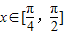 ,且不等式|f(x)-m|<2恒成立,求实数m的取值范围.
,且不等式|f(x)-m|<2恒成立,求实数m的取值范围.
【答案】分析:(1)先根据倍角公式,诱导公式及和差角公式,化简函数的解析式,将x=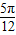 代入,可得答案.
代入,可得答案.
(2)根据(1)中函数的解析式,根据正弦函数的单调性,可求出f(x)的单调减区间;
(3)概据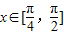 ,求出f(x)的值域,进而结合绝对值不等式的解法,求得不等式|f(x)-m|<2恒成立时,实数m的取值范围
,求出f(x)的值域,进而结合绝对值不等式的解法,求得不等式|f(x)-m|<2恒成立时,实数m的取值范围
解答:解:(1)∵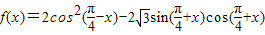
=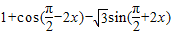
=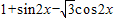 =
=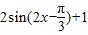 …(4分)
…(4分)
∴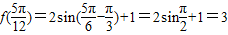 …(5分)
…(5分)
(2)由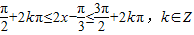 …(6分)
…(6分)
得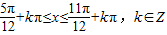 …(7分)
…(7分)
∴f(x)的单调减区间是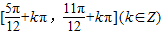 …(9分)
…(9分)
(3)∵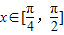 ,∴
,∴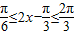 …(10分)
…(10分)
∴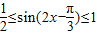 ,
,
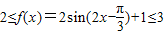 …(11分)
…(11分)
由|f(x)-m|<2得m-2<f(x)<m+2…(12分)
∴m-2<2且m+2>3,
即1<m<4…(14分)
点评:本题考查的知识点是二倍角的余弦公式,二倍角的正弦公式,两角差的正弦公式,三角函数的图象和性质,其中化简函数解析式为正弦型函数是解答的关键.
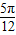 代入,可得答案.
代入,可得答案.(2)根据(1)中函数的解析式,根据正弦函数的单调性,可求出f(x)的单调减区间;
(3)概据
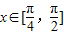 ,求出f(x)的值域,进而结合绝对值不等式的解法,求得不等式|f(x)-m|<2恒成立时,实数m的取值范围
,求出f(x)的值域,进而结合绝对值不等式的解法,求得不等式|f(x)-m|<2恒成立时,实数m的取值范围解答:解:(1)∵
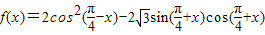
=
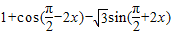
=
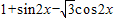 =
=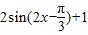 …(4分)
…(4分)∴
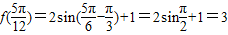 …(5分)
…(5分)(2)由
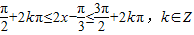 …(6分)
…(6分)得
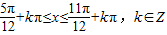 …(7分)
…(7分)∴f(x)的单调减区间是
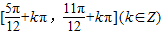 …(9分)
…(9分)(3)∵
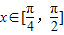 ,∴
,∴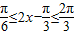 …(10分)
…(10分)∴
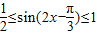 ,
,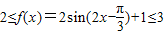 …(11分)
…(11分)由|f(x)-m|<2得m-2<f(x)<m+2…(12分)
∴m-2<2且m+2>3,
即1<m<4…(14分)
点评:本题考查的知识点是二倍角的余弦公式,二倍角的正弦公式,两角差的正弦公式,三角函数的图象和性质,其中化简函数解析式为正弦型函数是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的值;
的值;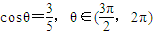 ,求
,求 .
. .
. 的值;
的值; .
. 的单调区间;
的单调区间; ,若对任意
,若对任意 ,总存在
,总存在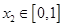 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.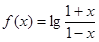 ,(1)求
,(1)求 的定义域;
(2)使
的定义域;
(2)使 的
的 的取值范围.
的取值范围. ,(1)求
,(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的集合。
的集合。