题目内容
定义域为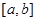 的函数
的函数 图象的两个端点为
图象的两个端点为 ,
, 是
是 图象上任意一点,其中
图象上任意一点,其中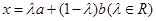 ,向量
,向量 ,若不等式
,若不等式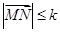 恒成立,则称函数
恒成立,则称函数 在
在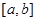 上“
上“ 阶线性近似”.若函数
阶线性近似”.若函数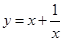 在
在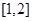 上“
上“ 阶线性近似”,则实数
阶线性近似”,则实数 的取值范围为( )
的取值范围为( )
A.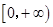 | B.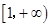 | C.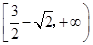 | D.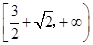 |
C
解析试题分析:函数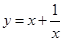 ,
, ,依题意
,依题意 ,
, ,
, ,
, (
( ),
), ,
,
由定义域为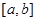 的函数
的函数 图象的两个端点为
图象的两个端点为 ,
, 是
是 图象上任意一点,其中
图象上任意一点,其中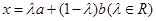 知:
知: ,令
,令 ,则
,则 ,所以
,所以 在
在 递减,
递减, 递增,从而有
递增,从而有 ,即
,即
从而 ,不等式
,不等式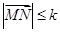 恒成立,则
恒成立,则
 ,故选择C,确定
,故选择C,确定 是解题正确的关键.
是解题正确的关键.
考点:参数范围及函数综合应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于
等于
A. | B. | C. | D.4 |
已知向量 满足
满足 ,则向量
,则向量 夹角的余弦值为 ( )
夹角的余弦值为 ( )
A.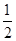 | B. | C. | D. |
在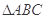 中,若
中,若 ,则
,则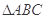 一定是( ).
一定是( ).
| A.钝角三角形 | B.锐角三角形 | C.直角三角形 | D.不能确定 |
已知向量 ,
, ,且
,且 ∥
∥ ,则tan α等于( )
,则tan α等于( )
A. | B.- | C. | D.- |
下列结论中,正确结论的个数是( )
(1)若 ,且
,且 ,则
,则
(2)
(3)
(4)若 ,
, ,
, ,
, ,
, 则
则 或
或
| A.0 | B.1 | C.2 | D.3 |
 ,
,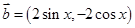 ,
,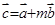 ,
, ,
,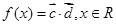 .
. 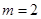 时,求
时,求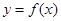 的取值范围;
的取值范围;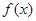 的最大值是
的最大值是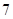 ,求实数
,求实数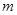 的值;
的值; 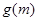 ,对任意的
,对任意的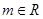 ,都有
,都有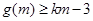 恒成立,求实数
恒成立,求实数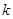 的取值范围.
的取值范围. 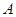 、
、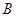 、
、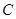 是
是 的内角,
的内角,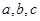 分别是其对边长,向量
分别是其对边长,向量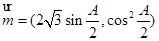 ,
,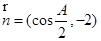 ,
,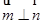 .
.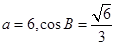 ,求
,求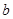 的长.
的长. ,
, ,
, ,求实数
,求实数 的值;
的值; ,求实数
,求实数