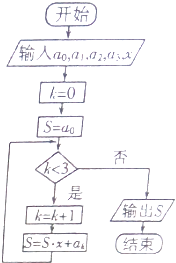
题目内容
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() (
(![]() ,
,![]() )与椭圆C交于两点A、B,点D满足
)与椭圆C交于两点A、B,点D满足![]() ,经过点D及点
,经过点D及点![]() 的直线的斜率为
的直线的斜率为![]() ,求证:
,求证:![]() .
.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】
(Ⅰ)设椭圆C的标准方程为![]() (a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为
(a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为![]() ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;
(Ⅱ)由题意知点D为线段AB的中点,设A(x1,y1),B(x2,y2),G(xD,yD),由题意知xD=﹣4kyD,![]() ,从而求出
,从而求出![]() ,进而得到
,进而得到![]() ,由此可知
,由此可知![]() .
.
(Ⅰ)设椭圆![]() 的标准方程为
的标准方程为![]() ,且
,且![]() .
.
由题意可知:![]() ,
,![]() .所以
.所以![]() .
.
所以,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)方法一:![]()
![]() ,点D为线段AB的中点
,点D为线段AB的中点
设![]()
![]() ,
,
 ,∴
,∴![]()
由![]() ,得
,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,∴
,∴![]() .
.
方法2:![]()
![]() ,点D为线段AB中点,
,点D为线段AB中点,
设![]()
![]() ,
, ,∴
,∴![]() ,
,
由![]() ,得
,得![]() ,
,
∵![]() ,∴
,∴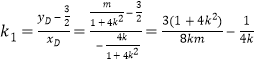 ,
,
![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() .
.
方法3:由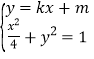 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
设![]() ,
,![]()
![]()
![]() ,点D为线段AB的中点,
,点D为线段AB的中点,
设![]() ,
,![]() ,
,
∵![]() ,∴
,∴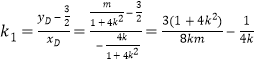 ,
,
![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目