题目内容
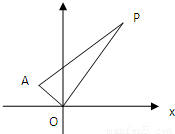
在平面直角坐标系xoy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA(1)求点P的轨迹C的方程
(2)若Q是轨迹C上异于点P的一个点,且
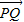 =λ
=λ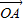 ,直线OP与QA交于点M.
,直线OP与QA交于点M.问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
【答案】分析:(1)设点P(x,y).由于kOP+kOA=kPA,利用斜率计算公式可得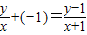 ,化简即为点P的轨迹方程.
,化简即为点P的轨迹方程.
(2)假设存在点P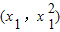 ,Q
,Q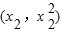 .使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
.使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
∵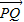 =λ
=λ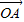 ,∴PQ∥OA,得kPQ=kAO=-1.于是
,∴PQ∥OA,得kPQ=kAO=-1.于是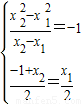 ,解出即可判断是否符合条件的点P存在.
,解出即可判断是否符合条件的点P存在.
解答:解:(1)设点P(x,y).∵kOP+kOA=kPA,∴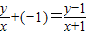 ,化为y=x2(x≠0,-1).即为点P的轨迹方程.
,化为y=x2(x≠0,-1).即为点P的轨迹方程.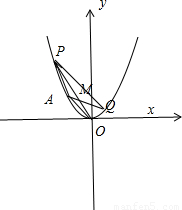
(2)假设存在点P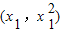 ,Q
,Q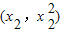 .使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
.使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
∵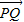 =λ
=λ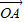 ,∴PQ∥OA,得kPQ=kAO=-1.
,∴PQ∥OA,得kPQ=kAO=-1.
∴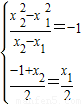 ,解得
,解得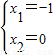 .此时P(-1,1),Q(0,0)分别与A,O重合,因此不符合题意.
.此时P(-1,1),Q(0,0)分别与A,O重合,因此不符合题意.
故假设不成立,及不存在满足条件的点P.
点评:熟练掌握抛物线的标准方程及其性质、斜率计算公式、中点坐标计算公式、三角形的面积计算公式、反证法等是解题的关键.
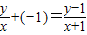 ,化简即为点P的轨迹方程.
,化简即为点P的轨迹方程.(2)假设存在点P
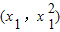 ,Q
,Q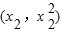 .使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
.使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.∵
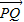 =λ
=λ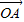 ,∴PQ∥OA,得kPQ=kAO=-1.于是
,∴PQ∥OA,得kPQ=kAO=-1.于是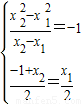 ,解出即可判断是否符合条件的点P存在.
,解出即可判断是否符合条件的点P存在.解答:解:(1)设点P(x,y).∵kOP+kOA=kPA,∴
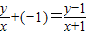 ,化为y=x2(x≠0,-1).即为点P的轨迹方程.
,化为y=x2(x≠0,-1).即为点P的轨迹方程.
(2)假设存在点P
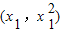 ,Q
,Q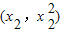 .使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.
.使得△PQA和△PAM的面积满足S△PQA=2S△PAM,则点M为线段AQ的中点.∵
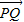 =λ
=λ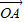 ,∴PQ∥OA,得kPQ=kAO=-1.
,∴PQ∥OA,得kPQ=kAO=-1.∴
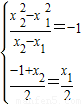 ,解得
,解得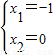 .此时P(-1,1),Q(0,0)分别与A,O重合,因此不符合题意.
.此时P(-1,1),Q(0,0)分别与A,O重合,因此不符合题意.故假设不成立,及不存在满足条件的点P.
点评:熟练掌握抛物线的标准方程及其性质、斜率计算公式、中点坐标计算公式、三角形的面积计算公式、反证法等是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是