题目内容

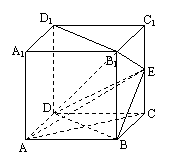
已知棱长为2的正方体ABCD-A1B1C1D1中，E为棱CC1的中点。

（1）求证：B1D1⊥AE；

（2）求证：AC//平面B1DE；

（3）求三棱锥A-BDE的体积。

（1）证明B1D1⊥面ACC1A1即可…………4分

（2）连AC1交B1D于O，连OE，证OE//AC即可。

     （方法很多）…………10分

（3）VA-BDE=…………14分

练习册系列答案
相关题目
已知棱长为2的正方体的八个顶点都在同一个球面上，求这个球的体积（　　）
A、
32
3
π
B、
8
2
3
π
C、4
3
π
D、24π
已知棱长为2的正方体ABCD-A1B1C1D1中，M为AB的中点，P是平面ABCD内的动点，且满足条件PD1=3PM，则动点P在平面ABCD内形成的轨迹是
 
．
已知棱长为2的正方体，内切球O，若在正方体内任取一点，则这一点不在球内的概率为
 
．
在区间（0，1）中随机地取出两个数，则两数之和小于
56
的概率是
 
．
已知棱长为2的正方体，内切球O，若在正方体内任取一点，则这一点不在球内的概率为
1-
π
6
1-
π
6
．
已知棱长为2的正方体的八个顶点都在同一个球面上，若在球内任取一点，则这一点q恰在正方体内的概率为（　　）
A、
3
4π
B、
3
2
2π
C、
2
3
3π
D、
1
3π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网