题目内容
已知在直角坐标系中(O为坐标原点),
=(2,5),
=(3,1),
=(x,3)
(I)若A、B、C可构成三角形,求x的取值范围;
(II)当x=6时,直线OC上存在点M,且
⊥
,求点M的坐标.
| OA |
| OB |
| OC |
(I)若A、B、C可构成三角形,求x的取值范围;
(II)当x=6时,直线OC上存在点M,且
| MA |
| MB |
分析:(1)若A、B、C可构成三角形,则
与
不共线,根据不共线向量坐标之间的关系求得x的取值范围.
(2)设
=λ
=(6λ,3λ),根据
•
=0得到关于λ的式子,求得λ的值即可.
| AB |
| BC |
(2)设
| OM |
| OC |
| MA |
| MB |
解答:解:(1)∵A、B、C可构成三角形,
∴A、B、C三点不共线,
即
与
不共线
而
=(1,-4),
=(x-3,2)
则有1×2+4×(x-3)≠0
即x的取值范围是x∈R且x≠
(2)∵
与
共线,故设
=λ
=(6λ,3λ),
又∵
⊥
,∴
•
=0
即45λ2-48λ+11=0,解得λ=
或λ=
∴
=(2,1)或
=(
,
)
∴点M的坐标为(2,1)或(
,
)
∴A、B、C三点不共线,
即
| AB |
| BC |
而
| AB |
| BC |
则有1×2+4×(x-3)≠0
即x的取值范围是x∈R且x≠
| 5 |
| 2 |
(2)∵
| OM |
| OC |
| OM |
| OC |
又∵
| MA |
| MB |
| MA |
| MB |
即45λ2-48λ+11=0,解得λ=
| 1 |
| 3 |
| 11 |
| 15 |
∴
| OM |
| OM |
| 22 |
| 5 |
| 11 |
| ,5 |
∴点M的坐标为(2,1)或(
| 22 |
| 5 |
| 11 |
| ,5 |
点评:本题考查了向量的共线与垂直以及向量的坐标运算,是基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程; 两点,求弦
两点,求弦 的长.
的长.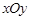 中,曲线
中,曲线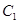 的参数方程为
的参数方程为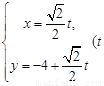 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点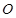 为极点,
为极点,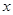 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线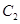 的方程为
的方程为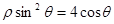 .
. ,求
,求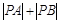 的值.
的值.