Question

求（)¹⁰的展开式中，系数的绝对值最大的项和系数最大的项.

Answer 1

答案：分析：在所有项的系数绝对值中，最大的一个必须满足“比它相邻的项都不小”这一必要条件，据此排列不等式组.而在讨论系数最大的项时，只需讨论奇数项即可.

解：展开式的通项是T_r+1=C·(-1)^r·2^-r·x.系数的绝对值是C·2^-r，若它最大，则

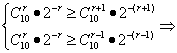
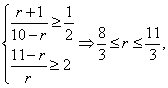
∵r∈N,∴r=3.

∴系数绝对值最大的项是第4项，即-C·2³·x=-15x.系数最大的项应在项数为奇数的项之内，即r取偶数0，2，4，6，8时，各项系数分别为C=1，C·2^-2=，C·2^-4=，·2 ^-6=，·2^-8=.因此系数最大的项是第5项，即.

提示：由于这个二项式的第二项分母中有数字2，所以展开式中的系数不是二项式系数，因此不能死背书上结论，以为中间项系数最大.