题目内容
已知函数y=sin2x+2sinxcosx+3cos2x,x∈R.(1)求该函数的单调增区间;
(2)求该函数的最大值及对应的x的值;
(3)求该函数的对称轴方程与对称中心坐标.
【答案】分析:(1)利用二倍角公式,降次升角,以及两角和的正弦函数,化简函数y=sin2x+2sinxcosx+3cos2x为y=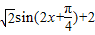 ,利用正弦函数的单调增区间,求该函数的单调增区间;
,利用正弦函数的单调增区间,求该函数的单调增区间;
(2)利用正弦函数的最值以及取得最值时的x值,直接求该函数的最大值及对应的x的值;
(3)利用正弦函数的对称轴和对称中心,直接求该函数的对称轴方程与对称中心坐标.
解答:解:y=sin2x+2sinxcosx+3cos2x=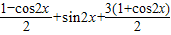
=sin2x+cos2x+2=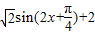 .(5分)
.(5分)
(1)由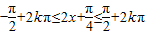 ,得
,得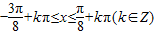 .
.
所以函数的单调增区间为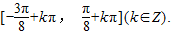 (8分)
(8分)
(2)令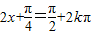 ,得
,得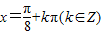 ,
,
所以当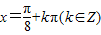 时,
时,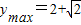 .(12分)
.(12分)
(3)由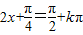 ,得
,得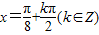 ,
,
所以该函数的对称轴方程为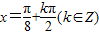 .
.
由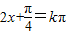 ,得
,得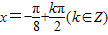 ,
,
所以,该函数的对称中心为: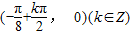 .(16分)
.(16分)
点评:本题是基础题,考查正弦函数的单调性,对称轴方程,对称中心,最值,利用基本函数的基本性质,是集合本题的关键,基本知识掌握的好坏,直接影响解题效果.
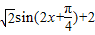 ,利用正弦函数的单调增区间,求该函数的单调增区间;
,利用正弦函数的单调增区间,求该函数的单调增区间;(2)利用正弦函数的最值以及取得最值时的x值,直接求该函数的最大值及对应的x的值;
(3)利用正弦函数的对称轴和对称中心,直接求该函数的对称轴方程与对称中心坐标.
解答:解:y=sin2x+2sinxcosx+3cos2x=
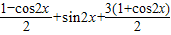
=sin2x+cos2x+2=
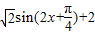 .(5分)
.(5分)(1)由
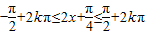 ,得
,得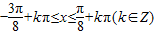 .
.所以函数的单调增区间为
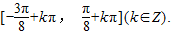 (8分)
(8分)(2)令
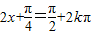 ,得
,得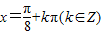 ,
,所以当
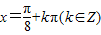 时,
时,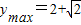 .(12分)
.(12分)(3)由
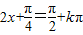 ,得
,得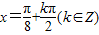 ,
,所以该函数的对称轴方程为
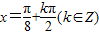 .
.由
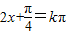 ,得
,得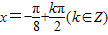 ,
,所以,该函数的对称中心为:
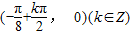 .(16分)
.(16分)点评:本题是基础题,考查正弦函数的单调性,对称轴方程,对称中心,最值,利用基本函数的基本性质,是集合本题的关键,基本知识掌握的好坏,直接影响解题效果.

练习册系列答案
相关题目



