题目内容
已知函数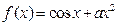 ,当
,当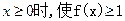 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个
正数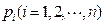 ,且
,且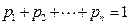 ,任取n个自变量的值
,任取n个自变量的值
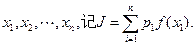
(I)求k的值;
(II)如果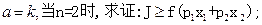
(III)如果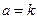 ,且存在n个自变量的值
,且存在n个自变量的值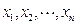 ,使
,使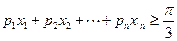 ,求证:
,求证: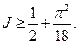
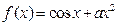 ,当
,当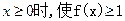 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个正数
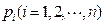 ,且
,且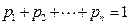 ,任取n个自变量的值
,任取n个自变量的值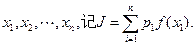
(I)求k的值;
(II)如果
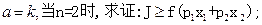
(III)如果
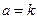 ,且存在n个自变量的值
,且存在n个自变量的值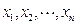 ,使
,使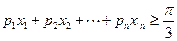 ,求证:
,求证: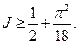
解:(Ⅰ)令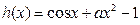 ,则
,则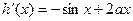 ,
,
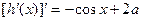 ,
,
当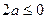 时,此时在
时,此时在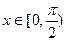 条件下,
条件下,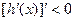 ,
,
则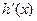 在
在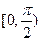 上为减函数,所以
上为减函数,所以 ,
,
所以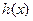 在
在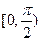 上为减函数,
上为减函数,
所以当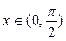 时,
时,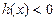 ,即
,即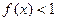 ;
;
当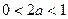 ,即
,即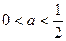 时,存在
时,存在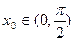 ,使得
,使得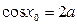 ,
,
当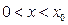 时,
时,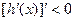 ,
,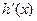 为减函数,则
为减函数,则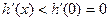 ,
,
即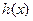 在
在 上递减,则
上递减,则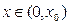 时,
时,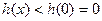 ,
,
所以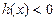 ,即
,即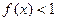 ; (2分)
; (2分)
当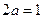 ,即
,即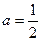 时,
时,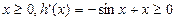 ,
,
则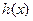 在
在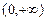 上为增函数,即当
上为增函数,即当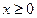 时,
时,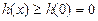 ,即
,即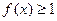 ;
;
当 ,即
,即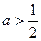 时,当
时,当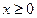 时,
时,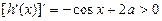 ,
,
则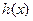 在
在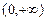 上为增函数,当
上为增函数,当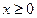 时,
时,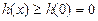 ,即
,即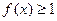 .
.
综上,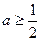 ,则
,则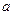 的最小值
的最小值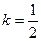 . (4分)
. (4分)
(Ⅱ)不妨设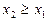 ,
,
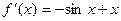 ,
,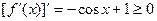 ,
,
所以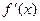 在
在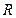 上为增函数, (5分)
上为增函数, (5分)
令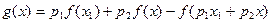 .
.
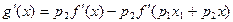 ,
,
当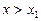 时, 因为
时, 因为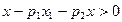 ,所以
,所以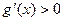 , (7分)
, (7分)
即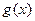 在
在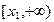 上为增函数,所以
上为增函数,所以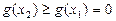 ,
,
则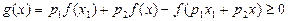 ,
,
则原结论成立. (8分)
(Ⅲ)(ⅰ)当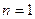 时,结论成立;
时,结论成立;
(ⅱ)假设当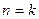 结论成立,即存在
结论成立,即存在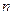 个正数
个正数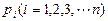 ,
,
 时,对于
时,对于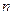 个自变量的值
个自变量的值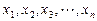 , 有
, 有
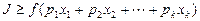 .
.
当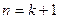 时,
时,
令存在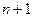 个正数
个正数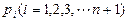 ,
, 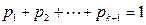 ,
,
令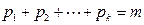 ,则
,则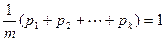 ,
,
对于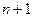 个自变量的值
个自变量的值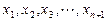 ,
,
此时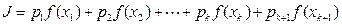
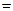
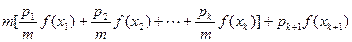
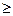
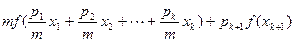 . (10分)
. (10分)
因为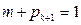 , 所以
, 所以
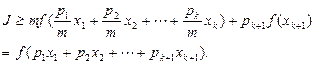
所以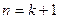 时结论也成立, (11分)
时结论也成立, (11分)
综上可得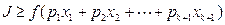 .
.
当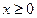 时,
时, 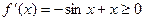 , (12分)
, (12分)
所以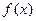 在
在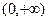 上单调递增,
上单调递增,
所以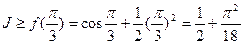
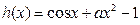 ,则
,则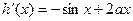 ,
,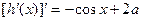 ,
,当
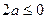 时,此时在
时,此时在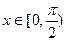 条件下,
条件下,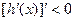 ,
,则
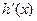 在
在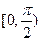 上为减函数,所以
上为减函数,所以 ,
,所以
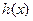 在
在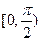 上为减函数,
上为减函数,所以当
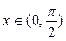 时,
时,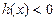 ,即
,即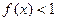 ;
;当
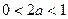 ,即
,即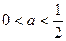 时,存在
时,存在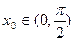 ,使得
,使得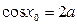 ,
,当
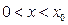 时,
时,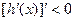 ,
,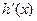 为减函数,则
为减函数,则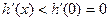 ,
,即
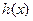 在
在 上递减,则
上递减,则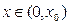 时,
时,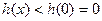 ,
,所以
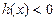 ,即
,即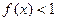 ; (2分)
; (2分)当
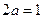 ,即
,即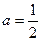 时,
时,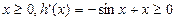 ,
,则
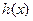 在
在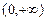 上为增函数,即当
上为增函数,即当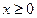 时,
时,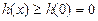 ,即
,即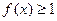 ;
;当
 ,即
,即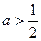 时,当
时,当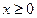 时,
时,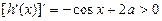 ,
,则
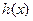 在
在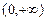 上为增函数,当
上为增函数,当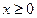 时,
时,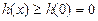 ,即
,即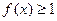 .
.综上,
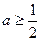 ,则
,则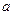 的最小值
的最小值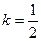 . (4分)
. (4分)(Ⅱ)不妨设
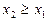 ,
,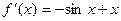 ,
,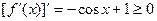 ,
,所以
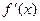 在
在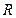 上为增函数, (5分)
上为增函数, (5分)令
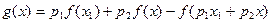 .
.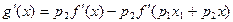 ,
,当
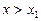 时, 因为
时, 因为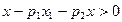 ,所以
,所以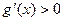 , (7分)
, (7分)即
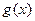 在
在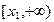 上为增函数,所以
上为增函数,所以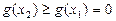 ,
,则
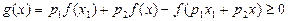 ,
,则原结论成立. (8分)
(Ⅲ)(ⅰ)当
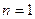 时,结论成立;
时,结论成立;(ⅱ)假设当
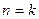 结论成立,即存在
结论成立,即存在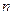 个正数
个正数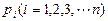 ,
, 时,对于
时,对于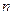 个自变量的值
个自变量的值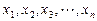 , 有
, 有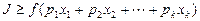 .
.当
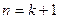 时,
时,令存在
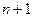 个正数
个正数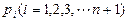 ,
, 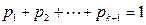 ,
,令
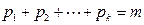 ,则
,则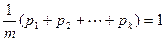 ,
,对于
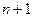 个自变量的值
个自变量的值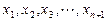 ,
,此时
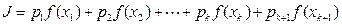
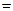
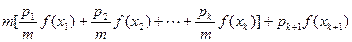
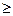
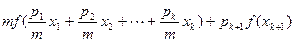 . (10分)
. (10分)因为
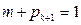 , 所以
, 所以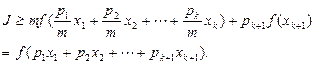
所以
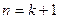 时结论也成立, (11分)
时结论也成立, (11分)综上可得
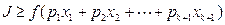 .
.当
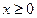 时,
时, 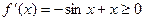 , (12分)
, (12分)所以
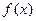 在
在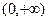 上单调递增,
上单调递增,所以
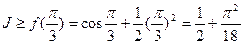
略

练习册系列答案
相关题目
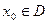 ,使
,使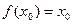 成立,则称以
成立,则称以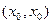 为坐标的点为函数
为坐标的点为函数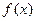 图象上的不动点。
图象上的不动点。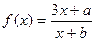 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求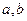 应满足的条件;
应满足的条件;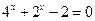 的解是
的解是  ,当2<a<3<b<4时,函数
,当2<a<3<b<4时,函数 的零点
的零点 ▲
▲ 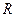 上的函数
上的函数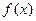 满足:①对任意
满足:①对任意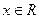 ,都有
,都有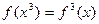 ;②对任意的
;②对任意的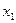 ,
,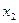
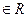 ,
,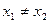 ,都有
,都有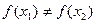 .那么
.那么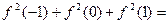

 其中b>2a,则不等式
其中b>2a,则不等式 ;
; 的两根为
的两根为 ,则
,则


