Question

如图示，已知直线l₁∥l₂，点A是l₁，l₂之间的一个定点，且A到l₁，l₂的距离分别为4、3，点B是直线l₁上的动点，若

AC

•

AB

=0，AC与直线l₂交于点C，则△ABC面积的最小值为（　　）

A．3

B．6

C．12

D．18

Answer 1

分析：过A作EF⊥l₁，与l₁交于E，与l₂交于F，设∠EAB=α，则∠FAC=90°-α，由A到l₁，l₂的距离分别为4、3，能够得到AB=

4

cosα

，AC=

3

cos(90°-α)

=

3

sinα

，所以△ABC的面积S=

12

sin2α

，由此知当α=45°时，sin2α=1，面积S获得最小值．

解答：解：如图，过A作EF⊥l₁，与l₁交于E，与l₂交于F，
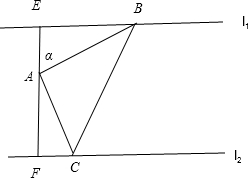
设∠EAB=α，则∠FAC=90°-α，
∵A到l₁，l₂的距离分别为4、3，
∴AE=4，AF=3，
∴AB=

4

cosα

，AC=

3

cos(90°-α)

=

3

sinα

，
∴△ABC的面积S=

1

2

AB•AC
=

1

2

×

4

cosα

×

3

sinα

=

12

sin2α

，
当α=45°时，sin2α=1，面积S获得最小值12．
故答案为：12．

点评：本题考查向量在几何中的灵活运用，综合性强，难度大，易出错．解题时要认真审题，注意三角函数性质的合理运用，恰当地作出图形，运用数形结合思想进行解题，有事半功倍之效．