题目内容
过点P（1，2）作直线l与圆（x-2）2+y2=9相交于A，B两点，那么|AB|的最小值为（ ）A．2
B．4
C．3
D．6
【答案】分析：由题中数据，算出点P是圆内的一点，根据圆的性质得当P与圆心的连线与AB互相垂直时，|AB|达到最小值．由此结合垂径定理加以计算，可得本题答案．
解答：解：∵P（1，2）满足（1-2）2+22=5＜9
∴点P是圆内的一点，
因此，当直线AB与CP互相垂直时，|AB|达到最小值（C为圆心（2，0））
∵|CP|=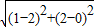
=
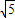
∴直线AB与CP互相垂直时，|AB|=2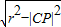
=2
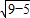=4
故选：B
点评：本题给出圆内一点P，求经过点P的直线被圆截得的最短弦长．着重考查了两点间的距离公式、圆的方程和圆的性质等知识，属于基础题．
解答：解：∵P（1，2）满足（1-2）2+22=5＜9
∴点P是圆内的一点，
因此，当直线AB与CP互相垂直时，|AB|达到最小值（C为圆心（2，0））
∵|CP|=
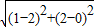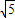
=∴直线AB与CP互相垂直时，|AB|=2
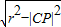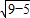=2=4故选：B
点评：本题给出圆内一点P，求经过点P的直线被圆截得的最短弦长．着重考查了两点间的距离公式、圆的方程和圆的性质等知识，属于基础题．
练习册系列答案
相关题目
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．