题目内容
设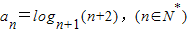 ,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .
,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .
【答案】分析:先利用换底公式与叠乘法把a1•a2•a3…ak化为log2(k+2),再根据a1•a2•a3…ak为整数,可得k=2n-2,进而由等比数列前n项和公式可得结论.
解答:解:∵an=logn+1(n+2)=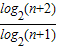
∴a1•a2•a3…ak= ×
× …×
…×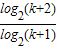 =log2(k+2),
=log2(k+2),
又∵a1•a2•a3…ak为整数
∴k+2必须是2的n次幂(n∈N*),即k=2n-2.
∴k∈[1,2009]内所有的企盼数的和M=(22-2)+(23-2)+(24-2)+…+(210-2)=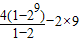 =2026
=2026
故答案为:2026.
点评:本题考查新定义,考查换底公式、叠乘法及等比数列前n项和公式,考查学生的计算能力,属于中档题.
解答:解:∵an=logn+1(n+2)=
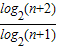
∴a1•a2•a3…ak=
 ×
× …×
…×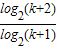 =log2(k+2),
=log2(k+2),又∵a1•a2•a3…ak为整数
∴k+2必须是2的n次幂(n∈N*),即k=2n-2.
∴k∈[1,2009]内所有的企盼数的和M=(22-2)+(23-2)+(24-2)+…+(210-2)=
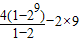 =2026
=2026故答案为:2026.
点评:本题考查新定义,考查换底公式、叠乘法及等比数列前n项和公式,考查学生的计算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
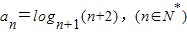 ,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .
,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 . a2
a2 a3
a3 …
… ak为整数的数k(k∈N+)叫做幸运数,则k∈[1,2011]内所有的幸运数的和为( ).
ak为整数的数k(k∈N+)叫做幸运数,则k∈[1,2011]内所有的幸运数的和为( ).