题目内容
已知函数f(x)= (x>0),设f(x)在点(n,f(n))(n∈N*)处的切线在y轴上的截距为bn,数列{an}满足:a1=
(x>0),设f(x)在点(n,f(n))(n∈N*)处的切线在y轴上的截距为bn,数列{an}满足:a1= N*).
N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)在数列 中,仅当n=5时,
中,仅当n=5时, 取最小值,求λ的取值范围;
取最小值,求λ的取值范围;
(Ⅲ)令函数g(x)=f(x)(1+x)2,数列{cn}满足:c1= ,cn+1=g(cn)(n∈N*),求证:对于一切n≥2的正整数,都满足:1<
,cn+1=g(cn)(n∈N*),求证:对于一切n≥2的正整数,都满足:1< <2.
<2.
解:(Ⅰ)∵ .则
.则 ,得
,得 ,即
,即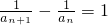 ,
,
∴数列 是以2为首项、1为公差的等差数列,
是以2为首项、1为公差的等差数列,
故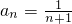 .(4分)
.(4分)
(Ⅱ)又∵ ,
,
∴函数f(x)在点(n,f(n))(n∈N*)处的切线方程为: ,
,
令x=0,得 .
.
∴ ,仅当n=5时取得最小值,
,仅当n=5时取得最小值,
只需 ,解得-11<λ<-9.
,解得-11<λ<-9.
故λ的取值范围为(-11,-9).(9分)
(Ⅲ)∵g(x)=f(x)(1+x)2=x(1+x),故cn+1=g(cn)=cn(1+cn),
又∵ ,故cn>0,则
,故cn>0,则 ,
,
即 .(11分)
.(11分)
∴
= .
.
又 =
= ,
,
故 .(14分)
.(14分)
分析:(Ⅰ)由 .和
.和 ,可得到
,可得到 最后由等差数列的定义求解即可.
最后由等差数列的定义求解即可.
(Ⅱ)通过求导得到切线的斜率,从而求得切线的方程, ,令x=0,可得
,令x=0,可得 .化简
.化简 由二次函数法求解即可.
由二次函数法求解即可.
(Ⅲ)结合(I)得g(x)=f(x)(1+x)2=x(1+x),所以cn+1=g(cn)=cn(1+cn),两边取倒数可得 .再由错位相消法化简问题论证即可.
.再由错位相消法化简问题论证即可.
点评:本题是函数、数列、不等式、导数等的大型综合题,情景新颖,具有较好的区分度,要求学生具有一定的审题、读题能力,一定的等价变形能力,是一种比较常见的题型,尤其数列不等式采用导数工具来处理的新题不可小视.
 .则
.则 ,得
,得 ,即
,即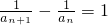 ,
,∴数列
 是以2为首项、1为公差的等差数列,
是以2为首项、1为公差的等差数列,故
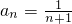 .(4分)
.(4分)(Ⅱ)又∵
 ,
,∴函数f(x)在点(n,f(n))(n∈N*)处的切线方程为:
 ,
,令x=0,得
 .
.∴
 ,仅当n=5时取得最小值,
,仅当n=5时取得最小值,只需
 ,解得-11<λ<-9.
,解得-11<λ<-9.故λ的取值范围为(-11,-9).(9分)
(Ⅲ)∵g(x)=f(x)(1+x)2=x(1+x),故cn+1=g(cn)=cn(1+cn),
又∵
 ,故cn>0,则
,故cn>0,则 ,
,即
 .(11分)
.(11分)∴

=
 .
.又
 =
= ,
,故
 .(14分)
.(14分)分析:(Ⅰ)由
 .和
.和 ,可得到
,可得到 最后由等差数列的定义求解即可.
最后由等差数列的定义求解即可.(Ⅱ)通过求导得到切线的斜率,从而求得切线的方程,
 ,令x=0,可得
,令x=0,可得 .化简
.化简 由二次函数法求解即可.
由二次函数法求解即可.(Ⅲ)结合(I)得g(x)=f(x)(1+x)2=x(1+x),所以cn+1=g(cn)=cn(1+cn),两边取倒数可得
 .再由错位相消法化简问题论证即可.
.再由错位相消法化简问题论证即可.点评:本题是函数、数列、不等式、导数等的大型综合题,情景新颖,具有较好的区分度,要求学生具有一定的审题、读题能力,一定的等价变形能力,是一种比较常见的题型,尤其数列不等式采用导数工具来处理的新题不可小视.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|