题目内容
(本题满分共14分)已知数列 ,
, ,且
,且 ,
,
(1)若 成等差数列,求实数
成等差数列,求实数 的值;(2)数列
的值;(2)数列 能为等比数列吗?若能,
能为等比数列吗?若能,
试写出它的充要条件并加以证明;若不能,请说明理由。
【答案】
解.(Ⅰ)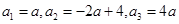 ,
,
因为 ,所以
,所以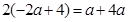 ,得
,得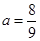
(Ⅱ)方法一:因为 ,所以
,所以 ,
,
得: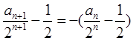 ,故
,故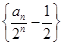 是以
是以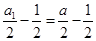 为首项,
为首项,
-1为公比的等比数列,
所以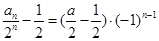 ,得:
,得: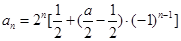
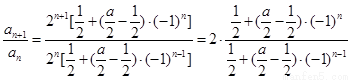
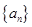 为等比数列
为等比数列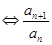 为常数,易得当且仅当
为常数,易得当且仅当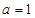 时,
时,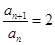 为常数。
为常数。
方法二:因为 ,所以
,所以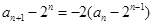 ,
,
即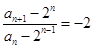 ,故
,故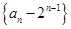 是以
是以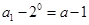 为首项,-2为公比的成等比数列,
为首项,-2为公比的成等比数列,
所以 ,得:
,得: (下同解法一)
(下同解法一)
方法三:由前三项成等比得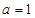 ,进而猜测
,进而猜测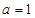 ,对于所有情况都成立,再证明。
,对于所有情况都成立,再证明。
【解析】略

练习册系列答案
相关题目
 ,它们的夹角为
,它们的夹角为 ,且
,且 ,
, ,
, 为正实数.
为正实数. 与
与 垂直,求
垂直,求 ;
; ,求
,求 的最小值及对应的
的最小值及对应的 与
与 是否垂直?
是否垂直? 为正四棱锥,几何体
为正四棱锥,几何体 为正四面体.
为正四面体. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
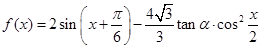 ,
,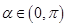 且
且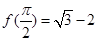 .
.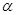 ;
;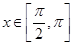 时,求函数
时,求函数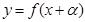 的值域.
的值域.