题目内容
已知实数x,y满足x+3y=1,则2x+8y的最小值为 .
【答案】分析:先判断2x与8y的符号,利用基本不等式建立关系,结合x+3y=1可求出2x+8y的最小值.
解答:解:由于2x>0,8y>0,所以
2x+8y=2x+23y≥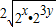
=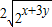
=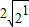
=2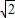
当且仅当2x=23y,x=3y,即x=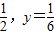 时取得最小值.
时取得最小值.
故答案为:2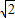
点评:本题主要考查了均值不等式的性质和应用,解题时要注意公式的正确应用,属于基础题.基本不等式求最值时要注意三个原则:一正,即各项的取值为正;二定,即各项的和或积为定值;三相等,即要保证取等号的条件成立.
解答:解:由于2x>0,8y>0,所以
2x+8y=2x+23y≥
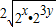
=
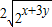
=
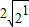
=2
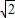
当且仅当2x=23y,x=3y,即x=
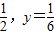 时取得最小值.
时取得最小值.故答案为:2
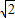
点评:本题主要考查了均值不等式的性质和应用,解题时要注意公式的正确应用,属于基础题.基本不等式求最值时要注意三个原则:一正,即各项的取值为正;二定,即各项的和或积为定值;三相等,即要保证取等号的条件成立.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|