题目内容
已知分别以d1和d2为公差的等差数列{an}和{bn}满足a1=18,b14=36,ak=bk=0,且a1,a2,a3…,ak,bk+1,bk+2,••,b14,…(k<14)的前n项和Sn满足S14=2Sk,则an+bn=
7n-70
7n-70
.分析:由已知中等差数列{an}和{bn}满足a1=18,b14=36,ak=bk=0,且S14=2Sk,根据等差数列的前n项公式,我们可以构造一个关于k的方程,解方程求出k值后,可得公差,进而得到两个数列的通项公式.
解答:解:∵S14=2Sk,
∴Sk=S14-Sk,
又∵ak=bk=0,a1=18,b14=36,
∴
×k=
×(14-k+1)
解得k=10
∴d1=-2,d2=9
则an=-2n+20,bn=9n-90
∴an+bn=7n-70
故答案为:7n-70
∴Sk=S14-Sk,
又∵ak=bk=0,a1=18,b14=36,
∴
| 18+0 |
| 2 |
| 36+0 |
| 2 |
解得k=10
∴d1=-2,d2=9
则an=-2n+20,bn=9n-90
∴an+bn=7n-70
故答案为:7n-70
点评:本题考查的知识点是数列的前n项和及等差数列的通项公式,其中根据已知求出k值及两个数列的公差是解答的关键.

练习册系列答案
相关题目
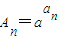 ,
,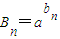 ,a>0且a≠1,探究不等式AnBn+1<An+Bn是否对一切正整数n恒成立?
,a>0且a≠1,探究不等式AnBn+1<An+Bn是否对一切正整数n恒成立?