Question

下图是根据y=f(x)绘出来的，则下列判断正确的是(    )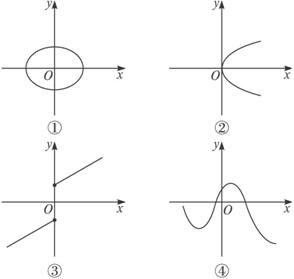

A.①的图象表示的函数y=f(x)既是奇函数又是偶函数

B.②的图象表示的函数y=f(x)是偶函数

C.③的图象表示的函数y=f(x)是奇函数

D.④的图象表示的函数y=f(x)既不是奇函数也不是偶函数

Answer 1

思路点拨：本题的考点是“根据函数的图象分析函数的奇偶性”，因此要先判断“图象”是不是函数图象，然后再判断.

解：①的图象表示的不是函数的图象，因为存在一个自变量x的取值(如:x=0)会有两个y与之对应，不符合函数的定义.因此A不正确.②的图象是关于x轴对称，既不符合偶函数的性质——图象关于y轴对称.也不符合函数的定义.因此B也不正确.③的图象是关于原点对称，但是当自变量x=0时，有两个y值与之对应，不符合函数的定义.所以C选项也不正确.④表示的图象符合函数的定义，因此它表示的是函数的图象，又由于它既不关于原点对称也不关于y轴对称，因此④的图象表示的函数既不是奇函数也不是偶函数.因此，选D.