题目内容
设函数f(x)是实数集上的奇函数,且满足f(x+1)=-f(x),当x∈(0,1)时,f(x)=log
(1-x),则f(x)在(1,2)上是( )
| 1 |
| 2 |
分析:令t=x-1,当x∈(1,2)时,t∈(0,1),f(x)=f(t+1)=-f(t)=-log
(2-x),故f(x)是减函数
且f(x)<0.
| 1 |
| 2 |
且f(x)<0.
解答:解:令t=x-1,则x=t+1,当x∈(1,2)时,t∈(0,1),
故f(x)=f(t+1)=-f(t)=-log
(1-t)=-log
(2-x).
当 x∈(1,2)时,log
(2-x)是增函数,f(x)=-log
(2-x)是减函数.
由x∈(1,2)知,0<2-x<1,log
(2-x)>0,f(x)=-log
(2-x)<0.
故选C.
故f(x)=f(t+1)=-f(t)=-log
| 1 |
| 2 |
| 1 |
| 2 |
当 x∈(1,2)时,log
| 1 |
| 2 |
| 1 |
| 2 |
由x∈(1,2)知,0<2-x<1,log
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查对数函数的定义域、值域及单调性,求函数的解析式,换元时注意变量范围的变化,这是解题的易错点.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
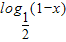 ,则f(x)在(1,2)上是( )
,则f(x)在(1,2)上是( )