题目内容
数列{an}满足条件an+2-2an+1+an=0,其前n项和为Sn,a10=30,a20=50.(1)求通项an;
(2)若Sn=242,求n的值.
解:(1)∵an+2-2an+1+an=0 ∴{an}成等差数列
∴an=a1+(n-1)d
由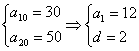
![]() an=2n+10
an=2n+10
(2)∵Sn=na1+![]() d
d
∴242=12n+![]() ·2
·2
![]() n=11或n=-22(舍)
n=11或n=-22(舍)
∴n=11

练习册系列答案
相关题目
题目内容
数列{an}满足条件an+2-2an+1+an=0,其前n项和为Sn,a10=30,a20=50.(1)求通项an;
(2)若Sn=242,求n的值.
解:(1)∵an+2-2an+1+an=0 ∴{an}成等差数列
∴an=a1+(n-1)d
由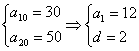
![]() an=2n+10
an=2n+10
(2)∵Sn=na1+![]() d
d
∴242=12n+![]() ·2
·2
![]() n=11或n=-22(舍)
n=11或n=-22(舍)
∴n=11
