题目内容
若3x,2x+1,2x+4是钝角三角形的三条边,则实数x的取值范围是 ( )
A. | B. |
C. | D. |
D
解析试题分析:当三边能构成三角形时 。若三角形为钝角三角形则最长边所对的角的余弦值小于0。当
。若三角形为钝角三角形则最长边所对的角的余弦值小于0。当 最长边为
最长边为 ,则
,则 ,整理得
,整理得 ,解得
,解得 ,所以
,所以 。当
。当 时,最长边为
时,最长边为 ,则
,则 ,整理得
,整理得 ,解得
,解得 或
或 ,所以
,所以 ,综上可得实数x的取值范围是
,综上可得实数x的取值范围是 。故D正确。
。故D正确。
考点:1三角形两边之和大于第三遍;2余弦定理。

练习册系列答案
相关题目
已知关于x的不等式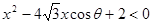 与
与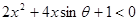 的解集,分别是
的解集,分别是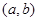 和
和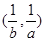 ,且
,且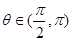 ,则
,则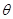 的值是( ).
的值是( ).
A.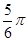 | B.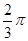 | C.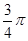 | D.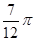 . . |
已知 ,不等式
,不等式 的解集为
的解集为 ,且
,且 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C. 或 或 | D. 或 或 |
不等式 的解集是 ( )
的解集是 ( )
A. | B. | C.(-2,1) | D. ∪ ∪ |
不等式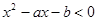 的解集为
的解集为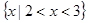 ,则不等式
,则不等式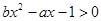 的解集为( )
的解集为( )
| A.(2,3) | B.(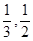 ) ) | C.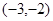 | D.(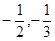 ) ) |
若不等式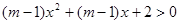 的解集是R,则m的范围是( )
的解集是R,则m的范围是( )
A.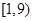 |
B. |
C.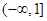 |
D. |
已知一元二次不等式f(x)<0的解集为 ,则f(10x)>0的解集为( ).
,则f(10x)>0的解集为( ).
| A.{x|x<-1或x>-lg 2} |
| B.{x|-1<x<-lg 2} |
| C.{x|x>-lg 2} |
| D.{x|x<-lg 2} |
“0<a<1”是“ax2+2ax+1>0的解集是实数集R”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
设函数f(x)=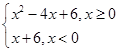 则不等式f(x)>f(1)的解集是( ).
则不等式f(x)>f(1)的解集是( ).
| A.(-3,1)∪(3,+∞) | B.(-3,1)∪(2,+∞) |
| C.(-1,1)∪(3,+∞) | D.(-∞,-3)∪(1,3) |