题目内容
已知命题p:|x2-x|≥6,q:x∈Z,且“p∧q”与“
q”同时为假命题，求x的值.
解：∵p∧q为假,∴p、q至少有一个为假.
又“q”为假,∴q为真,从而可知p为假.
由p为假且q为真,可得|x2-x|＜6且x∈Z,
即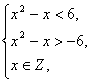
∴
∴
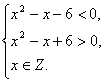
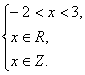故x的值为-1、0、1、2.
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
q”同时为假命题，求x的值.浙江名校名师金卷系列答案全优冲刺100分系列答案题目内容
已知命题p:|x2-x|≥6,q:x∈Z,且“p∧q”与“q”同时为假命题，求x的值.
解：∵p∧q为假,∴p、q至少有一个为假.
又“q”为假,∴q为真,从而可知p为假.
由p为假且q为真,可得|x2-x|＜6且x∈Z,
即∴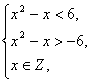
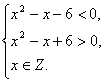
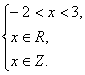∴故x的值为-1、0、1、2.
浙江名校名师金卷系列答案全优冲刺100分系列答案
p是