题目内容
Rt△ABC中,AB为斜边,
•
=9,S△ABC=6,设P是△ABC(含边界)内一点,P到三边AB,BC,AC的距离分别为x,y,z,则x+y+z的取值范围是
| AB |
| AC |
[
,4]
| 12 |
| 5 |
[
,4]
.| 12 |
| 5 |
分析:设三边分别为a,b,c,利用正弦定理和余弦定理结合向量条件利用三角形面积公式即可求出三边长.欲求x+y+z的取值范围,利用坐标法,将三角形ABC放置在直角坐标系中,通过点到直线的距离将求x+y+z的范围转化为x+y+z=
,然后结合线性规划的思想方法求出范围即可.
| m+2n+12 |
| 5 |
解答:解:△ABC为Rt△ABC,且∠C=90°,
设三角形三内角A、B、C对应的三边分别为a,b,c,
∵
(1)÷(2),得 tanA=
=
,
令a=4k,b=3k(k>0)
则 S△ABC=
ab=6⇒k=1∴三边长分别为3,4,5.
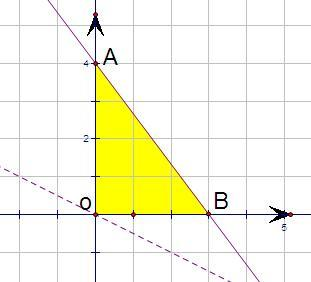 以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,
以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,
则A、B坐标为(3,0),(0,4),直线AB方程为4x+3y-12=0.
设P点坐标为(m,n),则由P到三边AB、BC、AB的距离为x,y,z.
可知 x+y+z=m+n+
,
且
,
故x+y+z=
,
令d=m+2n,由线性规划知识可知,如图:
当直线分别经过点A、O时,x+y+z取得最大、最小值.
故0≤d≤8,故x+y+z的取值范围是 [
,4].
故答案为:[
,4].
设三角形三内角A、B、C对应的三边分别为a,b,c,
∵
|
(1)÷(2),得 tanA=
| 4 |
| 3 |
| a |
| b |
令a=4k,b=3k(k>0)
则 S△ABC=
| 1 |
| 2 |
 以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,
以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,则A、B坐标为(3,0),(0,4),直线AB方程为4x+3y-12=0.
设P点坐标为(m,n),则由P到三边AB、BC、AB的距离为x,y,z.
可知 x+y+z=m+n+
| |4m+3n-12| |
| 5 |
且
|
故x+y+z=
| m+2n+12 |
| 5 |
令d=m+2n,由线性规划知识可知,如图:
当直线分别经过点A、O时,x+y+z取得最大、最小值.
故0≤d≤8,故x+y+z的取值范围是 [
| 12 |
| 5 |
故答案为:[
| 12 |
| 5 |
点评:本题主要考查了解三角形中正弦定理、余弦定理、平面向量数量积的运算、简单线性规划思想方法的应用,综合性强,难度大,易出错.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
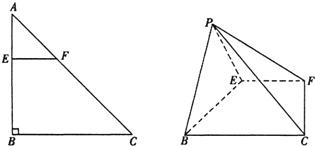
 如图,已知Rt△ABC 中,AB=AC=
如图,已知Rt△ABC 中,AB=AC=