题目内容
已知sinα=2cosβ,tanα=
解:由tanα=![]() ,得
,得![]() =
=![]() ,
,
把sinα=![]() cosβ代入得
cosβ代入得![]() ,
,
若cosβ=0,因为0<β<π,所以β=![]() ,
,
而此时sinα=0,因为-![]() <α<
<α<![]() ,
,
所以α=0,若cosβ≠0,则![]() sinβ=
sinβ=![]() cosα,cosα=
cosα,cosα=![]() sinβ,又sinα=
sinβ,又sinα=![]() cosβ,所以
cosβ,所以
sin2α+cos2α=![]() sin2β+2cos2β=1,
sin2β+2cos2β=1,
![]() (sin2β+cos2β)+
(sin2β+cos2β)+![]() cos2β=1,
cos2β=1,
![]() cos2β=
cos2β=![]() ,cos2β=
,cos2β=![]() ,
,
cosβ=±![]() ,sinα=±
,sinα=±![]() .
.
又因为-![]() <α<
<α<![]() ,0<β<π,
,0<β<π,
所以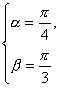 或
或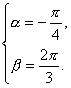
综上,满足条件的值有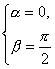 或
或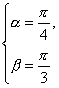 或
或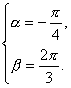

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目