题目内容
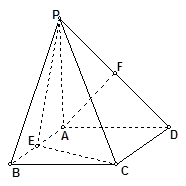
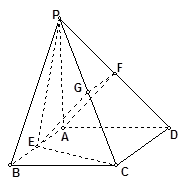
如图,四棱锥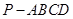 的底面是正方形,
的底面是正方形,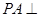 底面
底面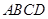 ,
,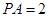 ,
,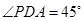 ,点
,点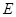 、
、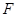 分别为棱
分别为棱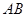 、
、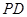 的中点.
的中点.
(1)求证: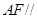 平面
平面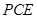 ;
;
(2)求证:平面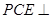 平面
平面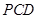 ;
;
(3)求三棱锥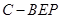 的体积.
的体积.
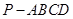 的底面是正方形,
的底面是正方形,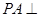 底面
底面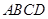 ,
,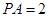 ,
,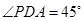 ,点
,点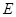 、
、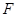 分别为棱
分别为棱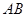 、
、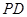 的中点.
的中点.
(1)求证:
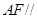 平面
平面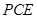 ;
;(2)求证:平面
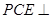 平面
平面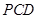 ;
;(3)求三棱锥
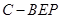 的体积.
的体积.(1)详见解析;(2)详见解析;(3)三棱锥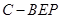 的体积为
的体积为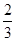 .
.
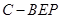 的体积为
的体积为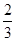 .
.试题分析:(1)取
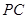 的中点
的中点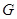 ,连接
,连接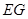 、
、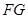 ,证明四边形
,证明四边形 为平行四边形,得到
为平行四边形,得到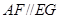 ,再利用直线平面平行的判定定理得到
,再利用直线平面平行的判定定理得到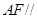 平面
平面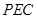 ;(2)先证明
;(2)先证明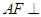 平面
平面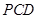 ,利用(1)中的条件
,利用(1)中的条件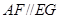 得到
得到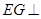 平面
平面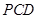 ,再利用平面与平面垂直的判定定理证明平面
,再利用平面与平面垂直的判定定理证明平面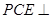 平面
平面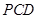 ,在证明
,在证明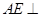 平面
平面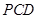 的过程中,在等腰三角形
的过程中,在等腰三角形 中利用三线合一得到
中利用三线合一得到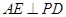 ,通过证明
,通过证明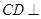 平面
平面 得到
得到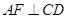 ,然后利用直线与平面垂直的判定定理即可证明
,然后利用直线与平面垂直的判定定理即可证明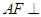 平面
平面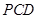 ;(3)利用题中的条件
;(3)利用题中的条件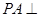 平面
平面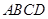 ,在计算三棱锥
,在计算三棱锥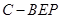 的体积中,选择以点
的体积中,选择以点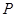 为顶点,
为顶点,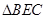 所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为
所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为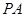 ,最后利用锥体的体积计算公式即可.
,最后利用锥体的体积计算公式即可.试题解析:(1)取
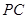 的中点
的中点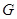 ,连结
,连结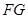 、
、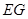 ,
, ∴
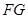 为
为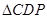 的中位线,
的中位线,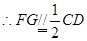 ,
,
∵四边形
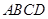 为矩形,
为矩形,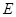 为
为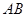 的中点,
的中点,∴
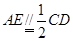 ,
,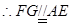 ,
, ∴四边形
 是平行四边形,
是平行四边形,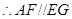 ,
,又
 平面
平面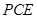 ,
,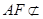 平面
平面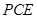 ,
,∴
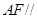 平面
平面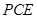 ;
;(2)
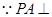 底面
底面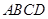 ,
, ,
,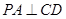 ,又
,又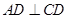 ,
,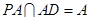 ,
,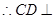 平面
平面 , 又
, 又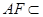 平面
平面 ,
, 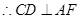 ,
,直角三角形
 中,
中,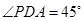 ,
,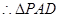 为等腰直角三角形,
为等腰直角三角形,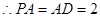 ,
,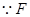 是
是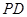 的中点,
的中点,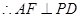 ,又
,又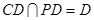 ,
,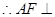 平面
平面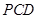 ,
, ,
,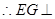 平面
平面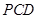 ,
,又
 平面
平面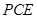 , 平面
, 平面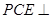 平面
平面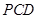 ;
; (3)三棱锥
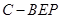 即为三棱锥
即为三棱锥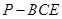 ,
,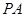 是三棱锥
是三棱锥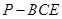 的高,
的高,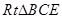 中,
中,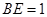 ,
,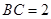 ,
, 三棱锥
三棱锥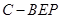 的体积,
的体积,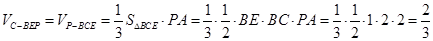 .
.
练习册系列答案
相关题目
 平面
平面 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
; ;
; 的体积.
的体积.
 ,底面面积为
,底面面积为 ,一条侧棱长为
,一条侧棱长为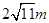 ,则它的侧面积为 .
,则它的侧面积为 .  的侧棱垂直于底面,各项点都在同一球面上,若
的侧棱垂直于底面,各项点都在同一球面上,若 ,
, ,
, ,
, ,则此球的表面积等于 .
,则此球的表面积等于 .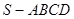 的所有棱长均为
的所有棱长均为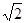 ,则过该棱锥的顶点
,则过该棱锥的顶点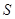 及底面正方形各边中点的球的体积为 .
及底面正方形各边中点的球的体积为 . ,则这个正方体的棱长是( )
,则这个正方体的棱长是( )







 中,已知
中,已知 是边长为1的正方形,且
是边长为1的正方形,且 是正三角形,,
是正三角形,, ,则该多面体的体积为( )
,则该多面体的体积为( )



