Question

设F₁、F₂分别是椭圆C:+=1(a＞b＞0)的左、右焦点,l为左准线,A₁、A₂分别为其长轴的左、右端点.

(1)若椭圆上的点M(1,)到F₁、F₂的距离之和为4,求椭圆方程;

(2)有一个猜想:“设P(x₁,y₁)、Q(x₂,y₂)(y₁y₂≠0)是椭圆C上的任意两点，若P、F₁、Q三点共线,则直线PA₁、QA₂、l共点.”你认为这个猜想能成立吗？请说明理由.

Answer 1

解：(1)由已知得,

2a=|MF₁|+|MF₂|=4,

∴a=2.又M在椭圆上,

∴+=1.

∴b=.

∴椭圆方程为+=1.

(2)由已知,A₁(-a,0)、A₂(a,0)、F₁(-c,0),直线PA₁的方程为y=(x+a),

    直线QA₂的方程为y=(x-a).

    设直线PA₁与l交于点P′(-,y_P′);直线QA₂与直线l交于Q′(-,y_Q′).

y_P′=(-+a),

y_Q′=(--a).

    要证PA₁、QA₂、l共点,只需证y_P′=y_Q′.

∵P、F₁、Q三点共线,

∴=.

∴c=.                                                                   ①

    由y_P′=y_Q′(-+a)=(--a)=,

    将①代入得y_P′=y_Q′.                                ②

    又∵点P、Q在椭圆C上,

∴

∴

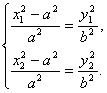
    两式相比得,

∴②恒成立.

∴恒有y_P′=y_Q′.

∴直线PA₁、QA₂、l恒共点.