题目内容
已知集合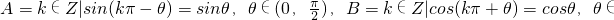 (0,
(0, )}.则(?ZA)∩B=
)}.则(?ZA)∩B=
- A.{k|k=2n,n∈Z}
- B.{k|k=2n-1,n∈Z}
- C.{k|k=4n,n∈Z}
- D.{k|k=4n-1,n∈Z}
A
分析:利用三角函数的诱导公式分别化简集合A,B,然后直接利用补集和交集的运算求解.
解答:由sin(kπ-θ)=sinθ,得k=2n+1,n∈Z.
所以A={k∈Z|sin(kπ-θ)=sinθ, }={k|k=2n+1,n∈Z}.
}={k|k=2n+1,n∈Z}.
则?ZA={k|k=2n,n∈Z}.
由cos(kπ+θ)=cosθ,得k=2n,n∈Z.
所以B={k∈Z|cos(kπ+θ)=cosθ, }={k|k=2n,n∈Z}.
}={k|k=2n,n∈Z}.
所以(?ZA)∩B={k|k=2n,n∈Z}.
故选A.
点评:本题考查了交、并、补集的混合运算,考查了三角函数的诱导公式,解答的关键是对三角函数诱导公式的记忆与运用,是基础题.
分析:利用三角函数的诱导公式分别化简集合A,B,然后直接利用补集和交集的运算求解.
解答:由sin(kπ-θ)=sinθ,得k=2n+1,n∈Z.
所以A={k∈Z|sin(kπ-θ)=sinθ,
 }={k|k=2n+1,n∈Z}.
}={k|k=2n+1,n∈Z}.则?ZA={k|k=2n,n∈Z}.
由cos(kπ+θ)=cosθ,得k=2n,n∈Z.
所以B={k∈Z|cos(kπ+θ)=cosθ,
 }={k|k=2n,n∈Z}.
}={k|k=2n,n∈Z}.所以(?ZA)∩B={k|k=2n,n∈Z}.
故选A.
点评:本题考查了交、并、补集的混合运算,考查了三角函数的诱导公式,解答的关键是对三角函数诱导公式的记忆与运用,是基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目