题目内容
将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3:4.再将它们卷成两个圆锥侧面,则两圆锥体积之比为
- A.3:4
- B.9:16
- C.27:64
- D.都不对
D
分析:设出圆形纸片的半径,根据两个扇形圆心角之比,得到扇形的弧长之比,得到两个圆锥的底面半径之比,得到两个圆锥的高之比,得到两个圆锥的体积之比,得到结果.
解答:设圆形纸片的半径是r,
∴沿半径剪开为两个扇形,其圆心角之比为3:4时,两个扇形的弧长分别是 ,
, ,
,
围成圆锥时两个圆锥的底面半径分别是 ,
, ,
,
两个圆锥的母线长度相等,都是r,
∴两个圆锥的高分别是 ,
,
两个圆锥的体积分别是
 ,
,

即两个体积为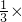
 ,
,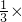

∴两个圆锥的体积之比是32 :9
:9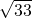 ,
,
故选D.
点评:本题考查旋转体中的圆锥,考查圆锥用扇形围成的过程中各个量之间的关系,本题是一个运算量比较大的题目,是一个中档题.
分析:设出圆形纸片的半径,根据两个扇形圆心角之比,得到扇形的弧长之比,得到两个圆锥的底面半径之比,得到两个圆锥的高之比,得到两个圆锥的体积之比,得到结果.
解答:设圆形纸片的半径是r,
∴沿半径剪开为两个扇形,其圆心角之比为3:4时,两个扇形的弧长分别是
 ,
, ,
,围成圆锥时两个圆锥的底面半径分别是
 ,
, ,
,两个圆锥的母线长度相等,都是r,
∴两个圆锥的高分别是
 ,
,
两个圆锥的体积分别是

 ,
,

即两个体积为
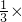
 ,
,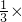

∴两个圆锥的体积之比是32
 :9
:9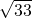 ,
,故选D.
点评:本题考查旋转体中的圆锥,考查圆锥用扇形围成的过程中各个量之间的关系,本题是一个运算量比较大的题目,是一个中档题.

练习册系列答案
相关题目
将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3:4.再将它们卷成两个圆锥侧面,则两圆锥体积之比为( )
| A、3:4 | B、9:16 | C、27:64 | D、都不对 |