题目内容
11.若数列{bn}的前n项和为Tn=2n+1,求数列{bn}的通项公式bn.分析 由数列的前n项和直接求出首项,结合bn=Tn-Tn-1(n≥2)求出n≥2时的通项公式,验证首项后得答案.
解答 解:由Tn=2n+1,得b1=T1=3;
当n≥2时,bn=Tn-Tn-1=2n+1-(2n-1+1)=2n-1.
验证n=1时上式不成立.
∴${b}_{n}=\left\{\begin{array}{l}{3,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.
点评 本题考查数列递推式,训练了由数列的前n项和求数列的通项公式,是基础题.

练习册系列答案
相关题目
1.不等式|1-x|<5的解集是( )
| A. | (-∞,-4)∪(6,+∞) | B. | [-4,6] | C. | (-4,6) | D. | (-6,4) |
6.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤1}\\{|l{g}{(x-1)}|,x>1}\end{array}\right.$,若关于x的方程f2(x)+bf(x)=0有4个不同的实根,则实数b的取值范围为( )
| A. | (2,+∞) | B. | (0,2] | C. | [-2,0) | D. | (-∞,-2) |
16.已知函数y=|x2-3x+2|,则( )
| A. | 有极小值,但没有极大值 | B. | 有极小值0,但没有极大值 | ||
| C. | 有极小值0,极大值$\frac{1}{4}$ | D. | 有极大值$\frac{1}{4}$,没有极小值 |
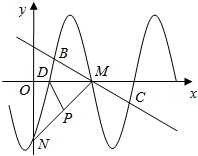 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).